入試問題において、伝説になっていると言ってもいい問題はいくつかありますが、その中でも群を抜いて有名だと言われているのが2003年に東京大学の数学の入試問題で出題されたこれでしょう。
円周率は3.05より大きいことを証明せよ。
東京大学(2003)
問題が1行!しかも、円周率が3.05より大きいだなんて、なんでこんな当たり前のことを聞くんだ…

ということで、この問題をタイトル通り、「中学生にもわかるように」解いていきたいと思います!
目次 (クリックでジャンプ)
その前に… なんでこの問題は有名なの?
解説を始める前に、”なぜ今問題が有名になったか”について触れて見たいと思います。
僕の考えるところ、理由は次の3つ!
問題を見たい方は読み飛ばしてください!
理由1. ゆとり教育では円周率が3だったから
今では考えられないかもしれませんが、ゆとり教育世代のある時期では、「円周率はだいたい3」と教わっていました。
これは、計算が面倒になるからという理由だったりします。
このことは、当時、世間では “子供の学力低下” につながるとして相当問題になりました。「円周率は3ではない」と嘆くドラマまであったとか。
そんな中、東大はこの「円周率は3.05より大きい」ことを示せという問題を出題したのです。これは、「円周率が3だと思っている生徒は東大にはいらない!」というメッセージの表れかもしれませんね!
理由2. どこぞの新聞の解答が間違えたから
僕は噂で聞いただけなのですが、この問題の解答速報が解答をミスってしまったらしいのです。
想像がつくかもしれませんが、相当物笑いのタネだったとか…

理由3. 東大入試の特徴が見えるから
東大の入試問題の特徴として、挙げられるのは、ズバリ
答えはわかるかもしれないけれど、それちゃんと意味までわかってる?
です。
この問題で言えば、円周率が3.14159… であることは今や誰もが知っていますが、「なぜ円周率が3.14159…なのか」について考えたことがある人はどれだけいるでしょうか?
東大では、こうした物事の本質に迫るような問題が出題されることがあるので「わかった気になった受験生」がどんどん落とされていきます。
だから、「とけた!」と思った問題でも意外と点数をもらえていないという事故が起きるのです。
問題を解いてみよう!
では、まずは問題を解いていきましょう。
問題文をもう一度確認してみます。
円周率は3.05より大きいことを証明せよ。
東京大学(2003)
さて、では証明していきましょう!
まず、すべきこと
この問題を見て、まず大体の人が思うこと、それは…

ってことです。
答えられる人いますか?
答えられない人は、円周率とは何か?ってことをしっかり理解しておきましょう!
円周率とは…
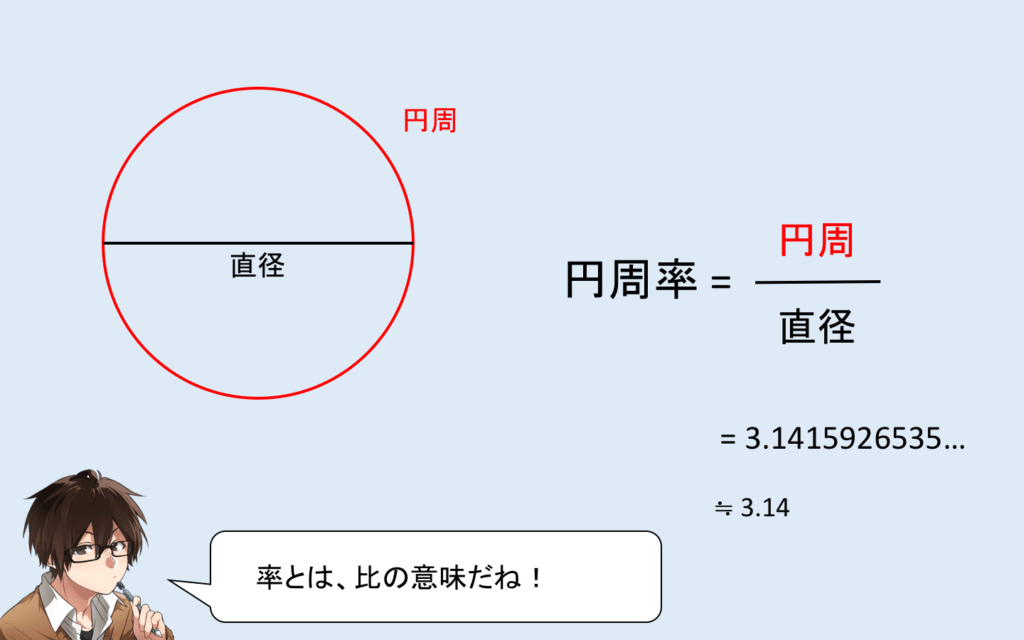
円周率とは、円周を直径で割ったものです。
円は、”定点 O からの距離が等しい点の集合でできる曲線” として定義されています。もう少し簡単に言えば、
中心からの距離(半径)が一定である図形
なのです。
注意して見て欲しいのは、定義の中に出てくる線分が半径だけということ。だから、半径(直径)が決まれば、円の形は決まってしまいます。
円の形が決まれば、円周も決まりますね!
つまり、直径が3とか12とかに決まれば、円周も “直径3の円の円周” とか、”直径12の円の円周” のように決まった値になります。
また、直径が2倍、3倍になると、直径も2倍、3倍になるのもわかりますか?
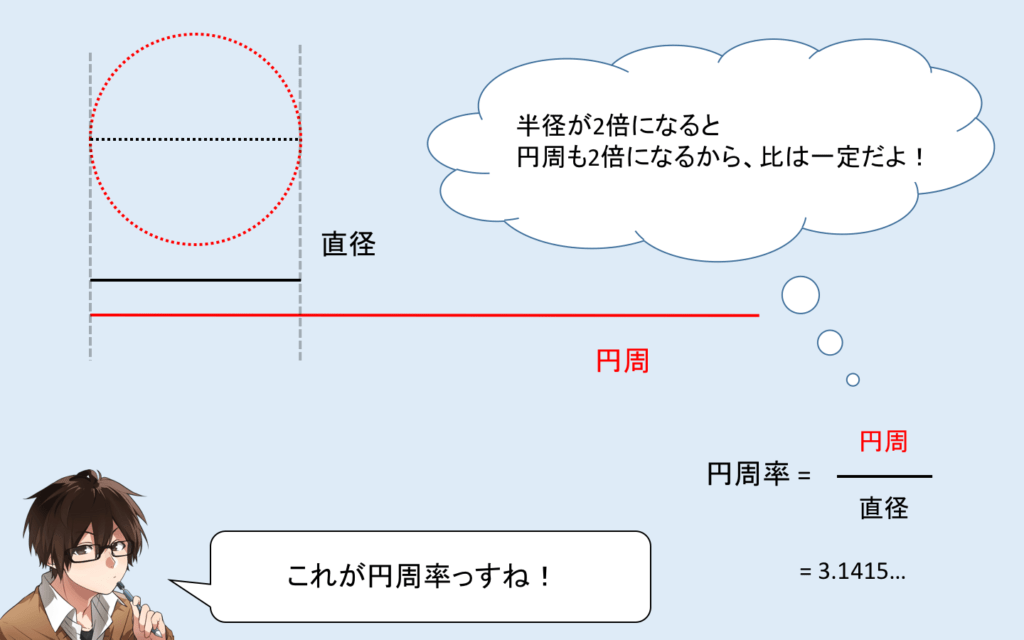
つまり、円周と半径の比は一定なのです!そしてそれ(直径です)が円周率( π )です!
式より、
円周 = 直径 × π
そして、この長さを評価しろというのが問題の趣旨なのです。
では、いきましょう!
求めたいものは…
問題から、求めたいものは
π > 3.05
です。つまり、円周率を何かそれより小さいものと比較して、それより大きいと言いたいのです。
方針としては、次のような感じ!
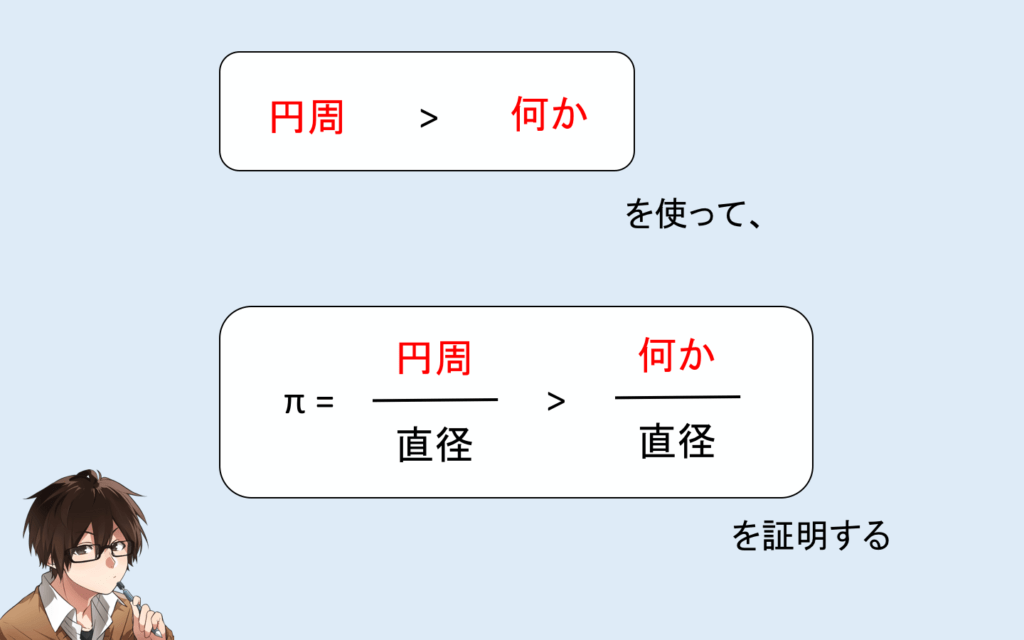
今回の問題のように、“〇〇より大きいことを証明せよ” とか、”〇〇以下であることを示せ” という問題では、何か簡単なものを使って「〇〇より〜ですよ!」と解答してあげます。これは結構良くある解法ですね。
さて、では円周より小さいものを用意しましょう!
まずは、正六角形でどうでしょう?
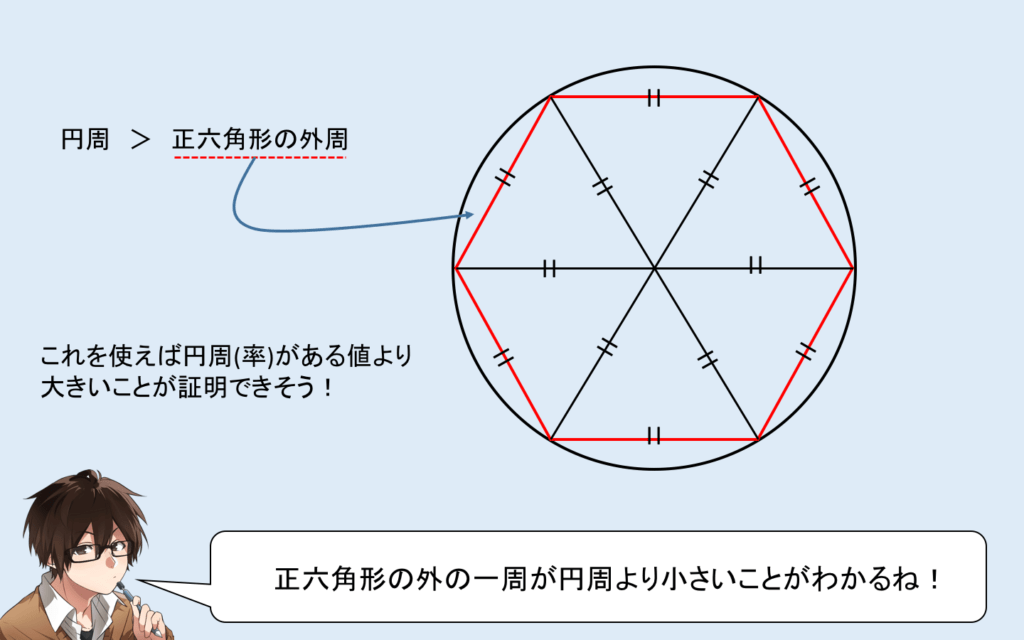
これを使うと、照明ができそうですね!
では、正六角形の長さを求めると…
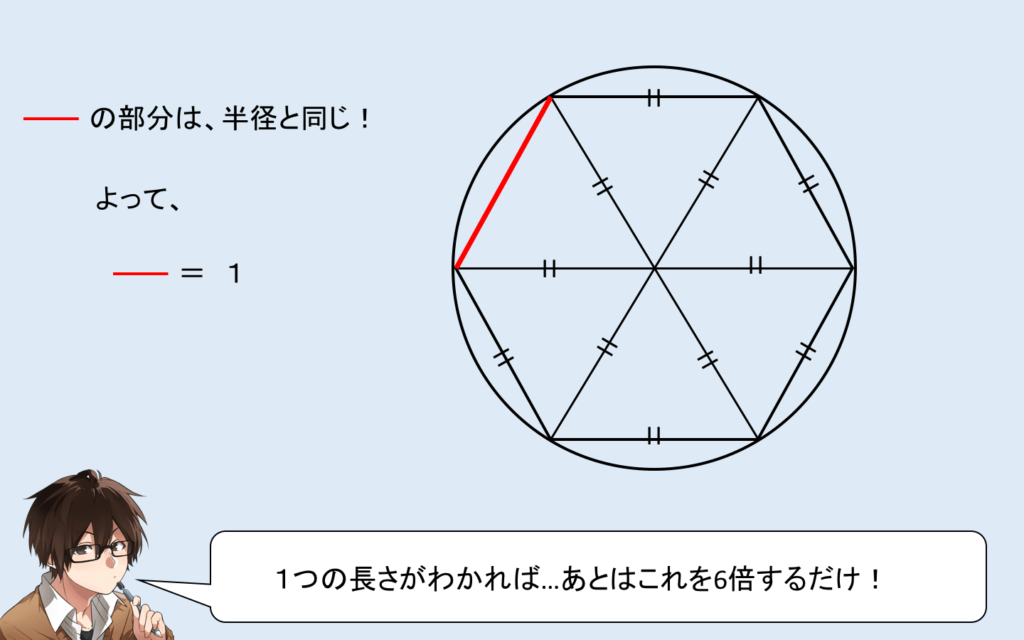
より、正六角形の長さ = 6 ですね!
よって、
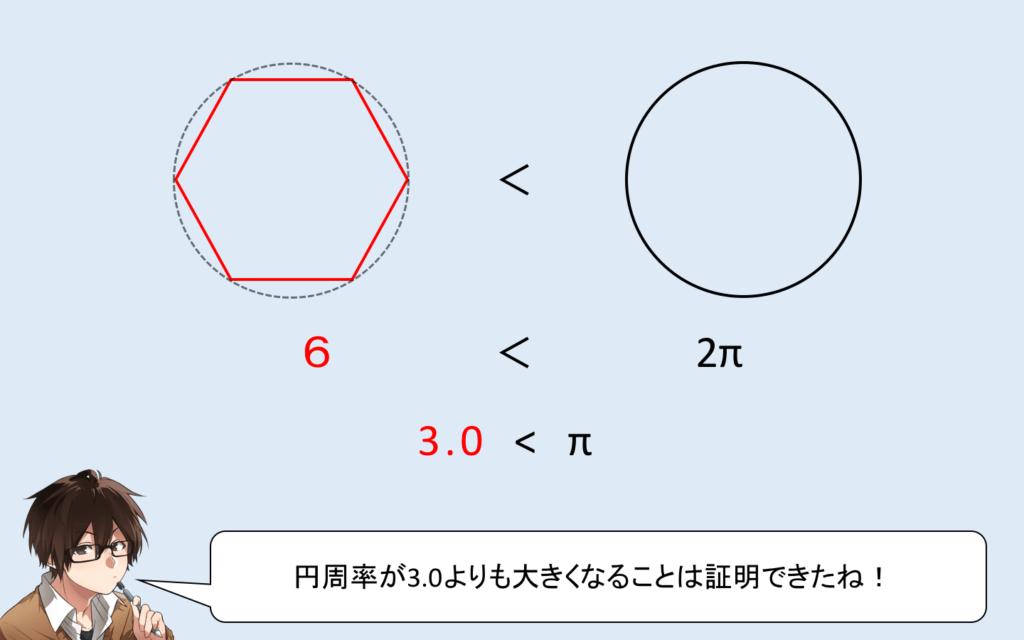
ただし…
これでは、
π > 3.05
を証明できてはいませんね…
つまり

ということです。
注目して欲しいのは2つ。
1つは、求めた “π > 3” は、円周率は3より大きいということです。つまり、ゆとり世代が学んでいた “円周率はおおよそ3” というのは間違ってはいないけれど、それではこの問題は解けないということです。
2つめは、正六角形では無理ならもっと円に近い図形ならどうかということです。円にどんどん図形を近づけていくと3.14…に近づいていくということが見えれば良いですね!
正八角形でやってみよう
では、正八角形でやってみましょう!
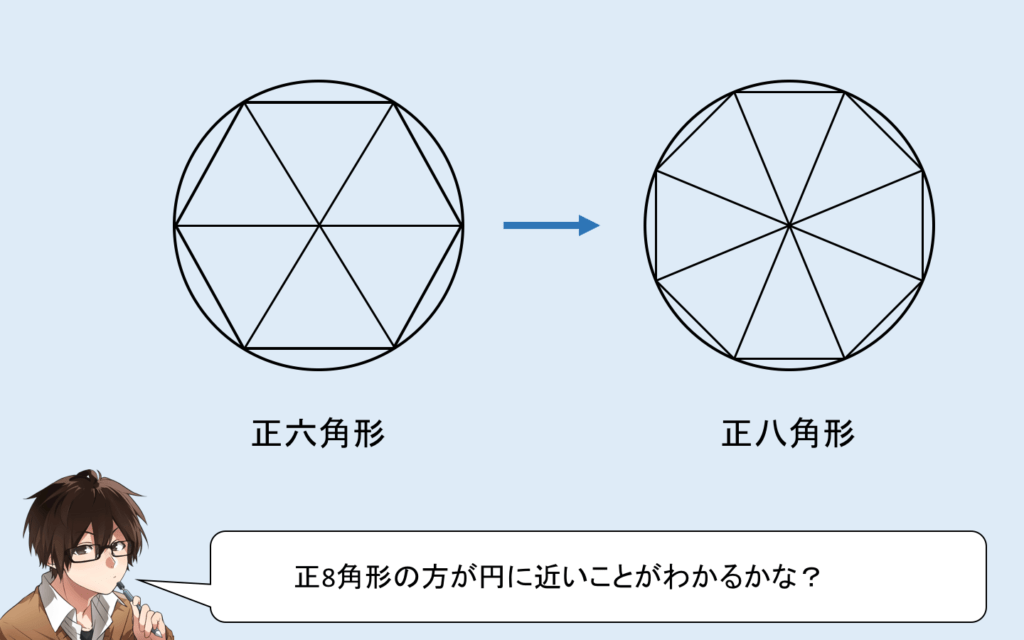
こっちだと、

これでいう “何か” が大きくなっています。ということは、π > 何か の部分が大きくなることに気がつきますか?
では、計算です!
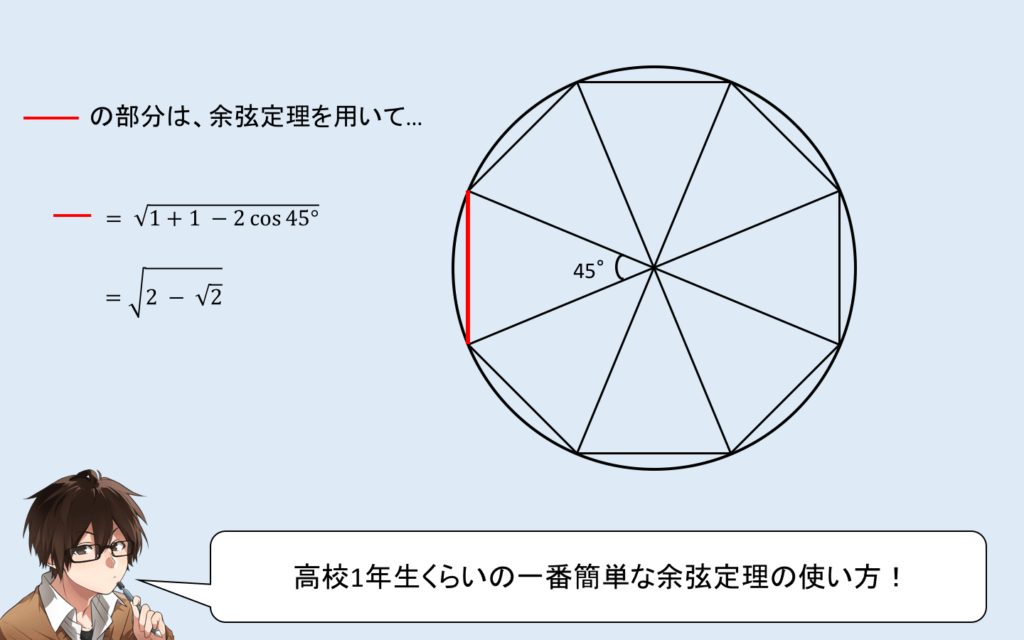
これを8倍したものと円周を比較して見ましょう!
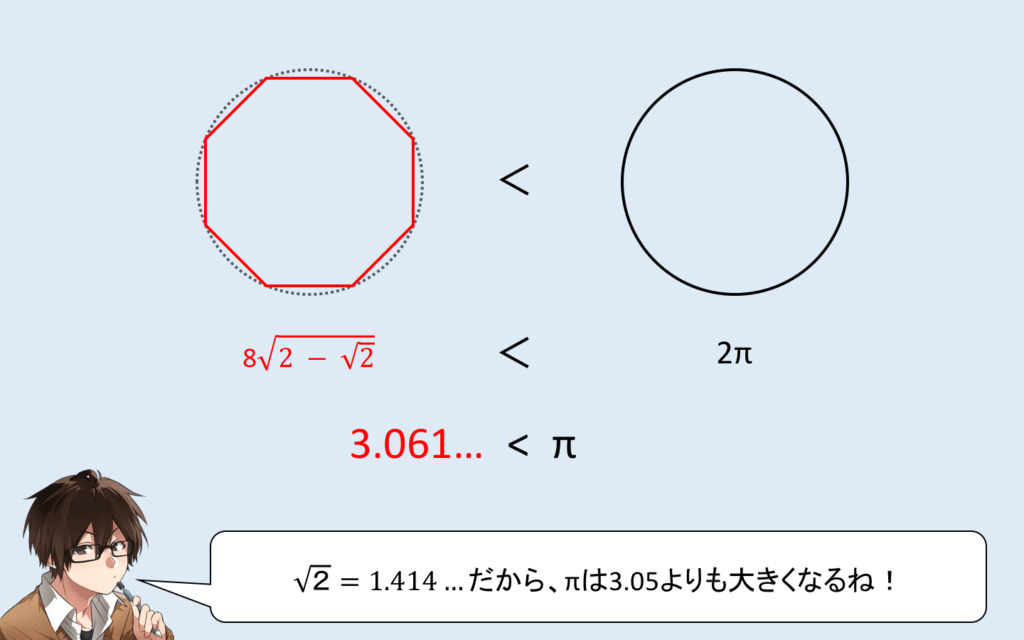
よって、これで
π > 3.05
が証明できましたね!

ちょっとまった!
さて、ここまで読んでいただいたあなたはお気づきかもしれませんが、余弦定理を使ってしまっているのでこれでは「中学生がわかるように」というタイトルどうりではありませんね!
そこで、別の方法も考えて見ましょう。
こちらはちゃんと中学生でも解くことができますよ!
要は長さが重要
上の例では、円周と正○角形を比較しましたが、要するに円周より短い長さがわかればいいのです。
では、適当に値をとってしまえばいいと思いますが、そこで問題が1つ
↓
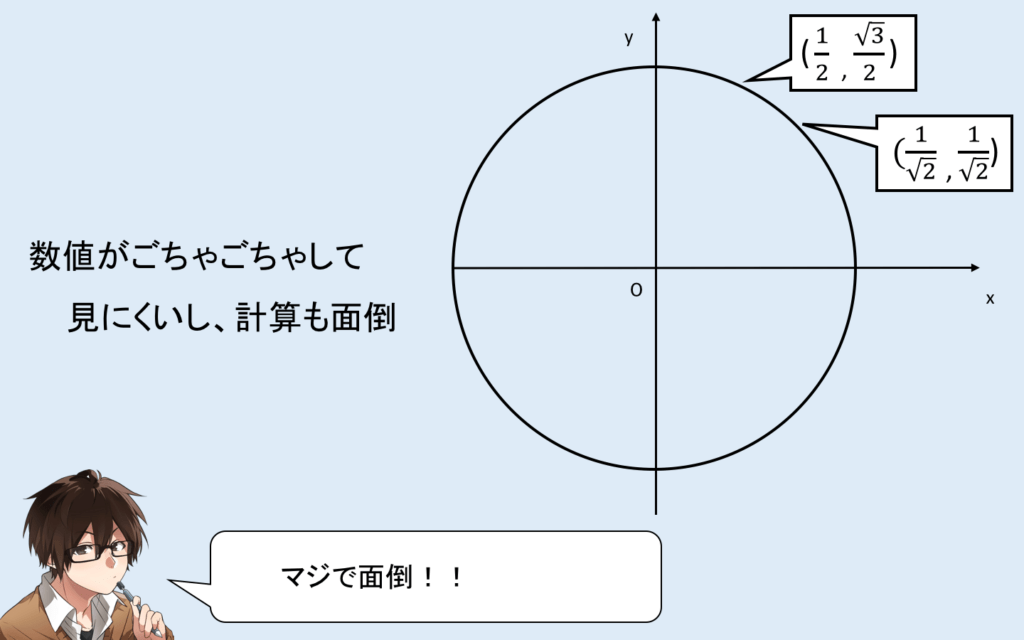
そう、面倒なのです。できなくはないのですが…
そこで、半径を5にしてみます。(なぜ5かというと…)
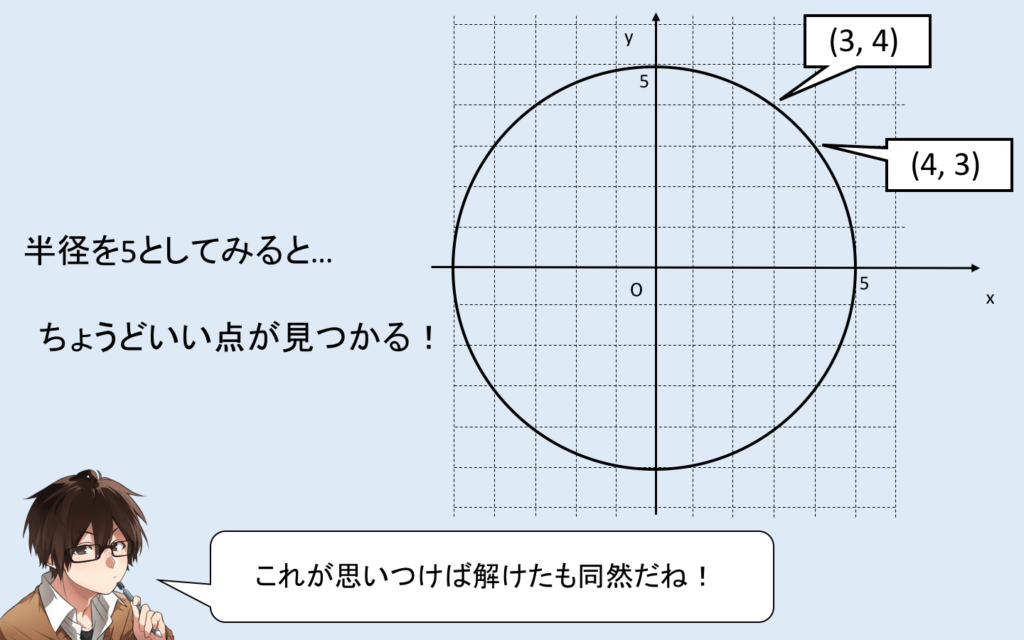
これがわかると、うまく線を引くことができれば長さを求めることができます!
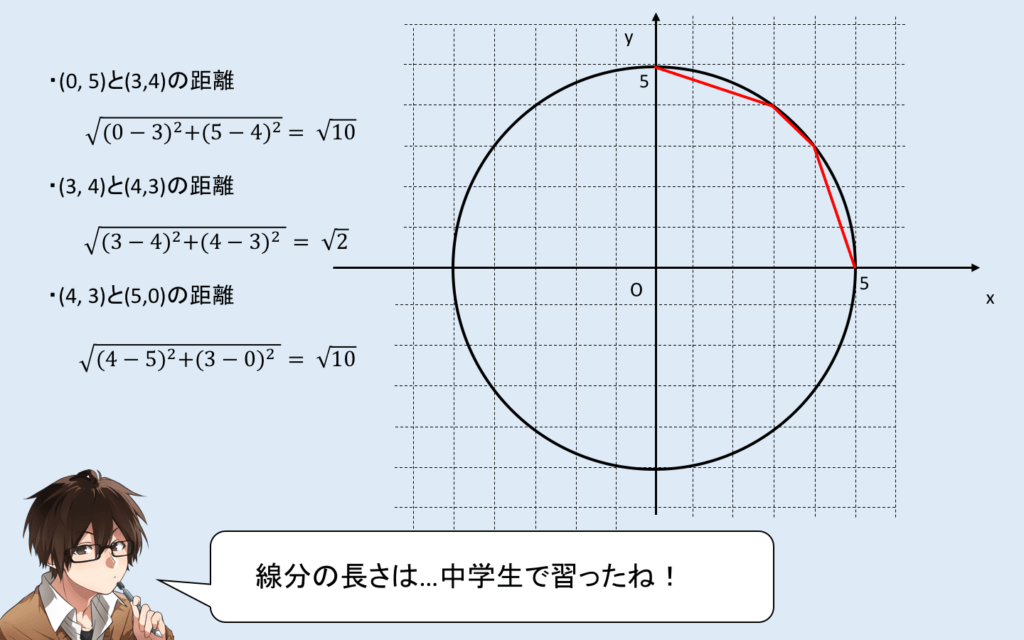
これは中学生でもできますね!
よって、これも4倍して、円周と比較しましょう!
円周が10πになっていることに注意すると…

どうですか?これが東大の問題ですよ?
大学生的解き方
さて、中学生はこんな感じで解くよ!ということは示すことができましたが、逆に大学生はどうしたらいいでしょう?
大学生は、なんだか裏技見たいなことを使います。
それは、マクローリン展開を用いるのですが…
それはまた今度証明しましょう。
注意したいこと
さて、ここまで東大の入試問題を解いてきましたが、注意したいことがあります。それは…

ということです。
この問題は2003年の問題の中では比較的簡単だったみたいですし、もし仮に試験会場でこの問題を見てすぐに解答できるかどうかということはまた別の話です!
だから、この問題だけを見て、

とは思わないでください!
しかし、

ということは事実ですね!
最後に
さて、東大の数学の入試問題である「円周率は3.05より大きいことを示せ」を中学生でもわかるように解説してきました!
理解できましたか?
スライドがかなり多くなってしまったのと、やはり直接教えるのではなくテキストとスライドでものを伝えようとするのは難しいのかな..?
何か質問だったり、訂正ポイントがあったりしたらコメントにてお願いします!
ちなみに、円周率とは不思議な数字で、無理数かつ超越数で、その小数展開は循環しません。つまり3.1415926535…と延々と続いていくということです。
ここから、最も重要な数学定数と言われていて、数学者の中には「円周率マニア」も結構いるそうです。
この本には、円周率が百万桁載っているというから驚きです。
また、円周率には未解決の問題も多く、
- π ± e は超越数か
- π は正規数か
などはいまだにわかっていません。
なんとも奥の深い数字ですね!
では、ここら辺で終わりです!
最後までお読みいただきありがとうございました!
以上、京大生ブロガーのいぶき(@ibuki_blogger )がお送りしました!























円周率のやつですが
4(2√10-√2)<10Πは間違えです
4(2√10+√2)<10Πが正しいです
訂正しました!ご指摘ありがとうございます!