アメリカなどにいくと、天気予報の温度の表示がアホみたいに高くて「なんだこりゃ!」と思ったことがある人は多いのではないでしょうか?
それもそのはずで、アメリカや一部の国では華氏(℉) が使われている地域があるからです。
僕も海外に行った時は、摂氏と華氏の変換がパッとできず、なかなか苦戦しました。
そこで、この記事では摂氏と華氏の変換をざっくりとやる方法から、正確な換算方法までをご紹介していきたいと思います!
目次 (クリックでジャンプ)
摂氏と華氏のだいたいの変換表
まずは、摂氏と華氏のざっくりとした換算表です。
| 華氏 (℉) | 摂氏(℃) | だいたいの感じ |
|---|---|---|
| 0 | -17.8 | 南極点の夏の最高気温くらい |
| 10 | -12.2 | モスクワの真冬の平均気温くらい |
| 20 | -6.7 | 北海道の冬の最低気温くらい |
| 30 | -1.1 | 都心での1年の最低気温くらい |
| 40 | 4.4 | 冬の東京都の平均気温くらい |
| 50 | 10.0 | 秋の終わりの日本列島くらい |
| 60 | 15.6 | 春や秋の陽気のイメージ |
| 70 | 21.1 | 初夏の爽やかな季節のイメージ |
| 80 | 26.7 | 少し暑いけど、気持ちの良いレベル |
| 90 | 32.2 | 暑い |
| 100 | 37.8 | めちゃめちゃ暑い |

オススメとしては、以下の数字を覚えておいて、そこからだいたいで計算すればいいと思います。
特にポイントは、
50 ℉ = 10 ℃ です。
「5010」と語呂合わせ(?) で覚えておくだけで、天気予報をパッとみただけでだいたいどんな感じかわかるようになりますよ!
摂氏と華氏の変換のやり方 (公式)

それでは、今度は正確な数字の換算方法をお伝えしたいと思います。
やり方は単純で、ズバリ「公式に入れるだけ」です。
$$ ℃ = \frac{(℉ – 32)}{1.8} $$
計算は単純で、℉から32を引いて、1.8 を掛けるだけ!
ちなみに、これを逆に解くと、摂氏から華氏の換算もできるようになります。
$$ ℉ = (1.8 × ℃) + 32 $$
計算方法そのものは単純です。
では、一応正式な変換の表も載せておきたいと思います。小数点は2桁までです。
華氏 を0℉から 5づつ刻んだ表です。
| 華氏 (℉) | 摂氏 (℃) |
|---|---|
| 0 | -17.8 |
| 5 | -15.0 |
| 10 | -12.2 |
| 15 | -9.4 |
| 20 | -6.7 |
| 25 | -3.9 |
| 30 | -1.1 |
| 35 | 1.7 |
| 40 | 4.4 |
| 45 | 7.2 |
| 50 | 10.0 |
| 55 | 12.8 |
| 60 | 15.6 |
| 65 | 18.3 |
| 70 | 21.1 |
| 75 | 23.9 |
| 80 | 26.7 |
| 85 | 29.4 |
| 90 | 32.2 |
| 95 | 35.0 |
| 100 | 37.8 |
摂氏を 0℃から5づつ刻んだ表です。
| 摂氏 (℃) | 華氏 (℉) |
|---|---|
| 0 | 32 |
| 5 | 41 |
| 10 | 50 |
| 15 | 59 |
| 20 | 68 |
| 25 | 77 |
| 30 | 86 |
| 35 | 95 |
| 40 | 104 |
| 45 | 113 |
| 50 | 122 |
| 55 | 131 |
| 60 | 140 |
| 65 | 149 |
| 70 | 158 |
| 75 | 167 |
| 80 | 176 |
| 85 | 185 |
| 90 | 194 |
| 95 | 203 |
| 100 | 212 |
とはいえ、これを正確に覚えておいたり、暗算でパッと解くのは難しいですよね…
そこで、普段使うような 0℃ ~ 100℃ くらいの間で、だいたい近くなるような近似式を紹介したいと思います!
摂氏と華氏のだいたいの変換の仕方

暗記で摂氏と華氏を変換するのはとても大変ですが、ここではだいたいざっくりと変換できるようになる裏技をご紹介したいと思います!
それが、こちらの式です!
$$ ℃ = (℉ – 30) / 2 $$
華氏から30 を引いて、2で割るだけ!

グラフにしてみると、-10℃ ~ 100℃ くらいの間でだいたい近いような値になっていると思います。(横軸が華氏、縦軸が摂氏になっています。)
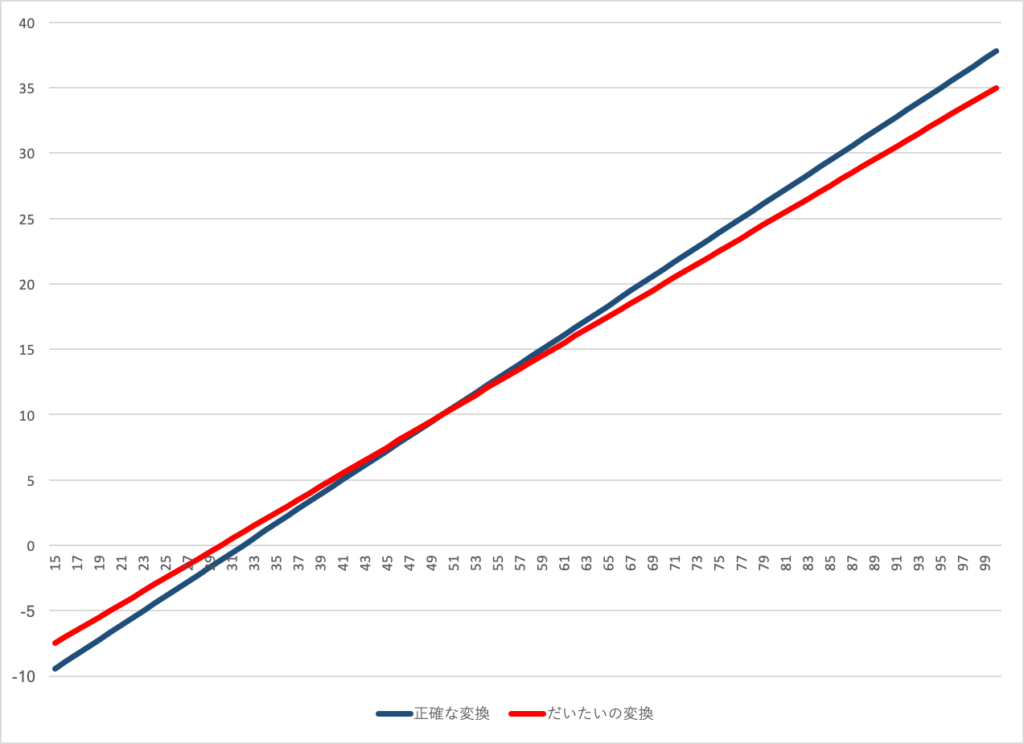
fig 1 正確な変換とだいたいの変換のグラフ
青い線が正確な変換の式を使って変換したもの、赤い線がざっくりの式を使って出したものです。
一番左の端っこの15℉ で正確な値が -11.7℃ に対して、ざっくりの方が -9.5℃ 、一番右の端では 99℉ の正確な値は37.8 ℃ に対して、ざっくりの方が 35℃なので、100 ℃以上の幅で、誤差は高々 2℃程度。
しかも、普段使う50 ℉ あたりのところではもっと正確なので、試験や学問で使う以外には特に問題はないと思います。
暗記するのもそんなに大変じゃないし、暗算も結構簡単にできるのでオススメ。
これは、僕は日常で結構使っているので、ぜひ覚えてみてください!
ケルビンと華氏の関係も簡単にわかる
摂氏(℃) とケルビンには、以下のような関係式がありました。
$$ K = ℃ + 273 $$
では、華氏(℉) とケルビンにはどのような関係があるでしょうか?
これは先程までの話がわかっていれば簡単で、摂氏のところに$ K – 273# を代入してやると、答えが簡単に求まって…
$$ K = \frac{ (℉ – 32)}{1.8} + 273 $$
がわかると思います。
このように、上の基本的な関係式から全てのことがわかるので、覚えられそうな人は正確な式も暗記してみるようにしましょう!
マル秘話:なぜアメリカは華氏を使うの?
華氏は、英語ではファーレンハイト(Fahrenheit) と言います。(他方で、摂氏はセルシウス Celcius を使います)
ここまで計算してきてくれた人は、

と思った人も多いと思います。なぜ、アメリカは温度を華氏で表示しているんでしょうか?
疑問に思って調べてみたのですが、これはどうも温度のことだけではなくて、アメリカは単位がほとんど自前のものみたいです…
- 長さ… ヤード (世界標準はメートル)
- 重さ… ポンド (世界標準はグラム)
こんな感じで、とにかく自前の単位を使っていて、なかなか統一が難しいそうです。
まぁ、僕たち部屋の大きさを表す時に「4畳半」と言ったりするので慣れていないものを使うのは大変なのかなぁと思いました。
まとめ:摂氏と華氏の変換は、公式に当てはめよう
以上が摂氏と華氏の変換のポイントとやり方でした。
まとめると、以下のようになります!
- 華氏から摂氏への変換は、$ ℃ = \frac{ (℉ – 32) }{1.8}$ を使う
- 覚えておきたい数字は、50 ℉ = 10 ℃
- だいたいで良いなら、$ ℃ = (℉ – 30) / 2 $ を使えるようになると便利
これだけ覚えておけば、海外に行って天気予報を見たりしても全然大丈夫ですね!
なので、紙に書き写すなり、スマホに送るなどしてこれだけはぜひ暗記して自分の知識にできるようにしてみてください!