数学IAの中でも、絶対に覚えておきたい項目がいくつかありますが、その中でも重要なものが余弦定理です。
この定理は、覚えづらかったり何に使うかよくわからないことが多いのですが、かなり頻繁に出てくるので理解できないと先に進みません。
そこで、この記事では余弦定理の証明や使い方をイラスト付きで解説していきたいと思います。3分ほどでざっくりと理解できるようになっています。
定期テストやセンター試験にも頻出なので、この記事を読んでしっかりと理解しておきましょう!
目次 (クリックでジャンプ)
余弦定理の公式
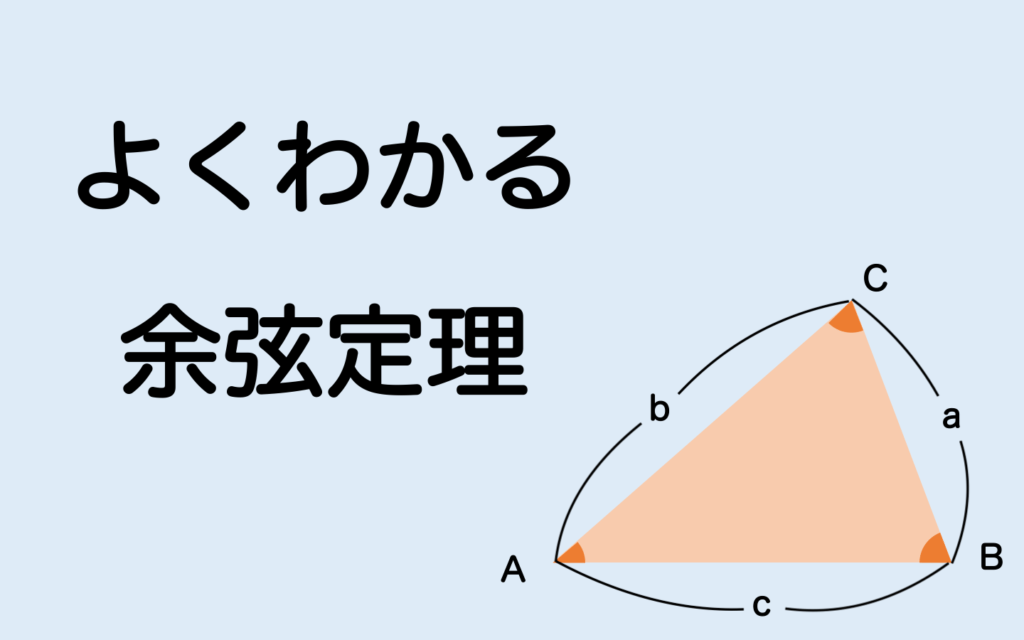
下の図のような三角形において、
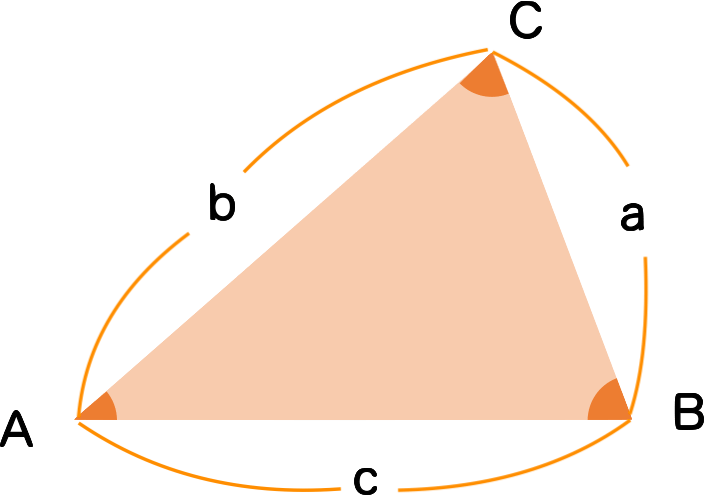
$$ a^2 = b^2 + c^2 – 2bc \cos A $$
$$ b^2 = c^2 + a^2 – 2ca \cos B $$
$$ c^2 = a^2 + b^2 – 2ab \cos C $$
が成り立つことを言います。
覚え方としては、「2辺挟角(2辺とその間の角)を使って、反対側の辺の長さを求める」としておけばいいと思います。また、角度が90°の時、cos = 0 となるので
$$ a^2 = b^2 + c^2 $$
となります。これはピタゴラスの定理と同じなので間違えることはないでしょう。
ちなみに、変形しておいて、
$$\cos A = \frac {b^2 + c^2 – a^2}{2bc} $$
という式を余弦定理ということもあります。
余弦定理の証明
図を使って証明をしていきたいと思います。
角A,B,C と辺a,b,c を図のようにおきます。
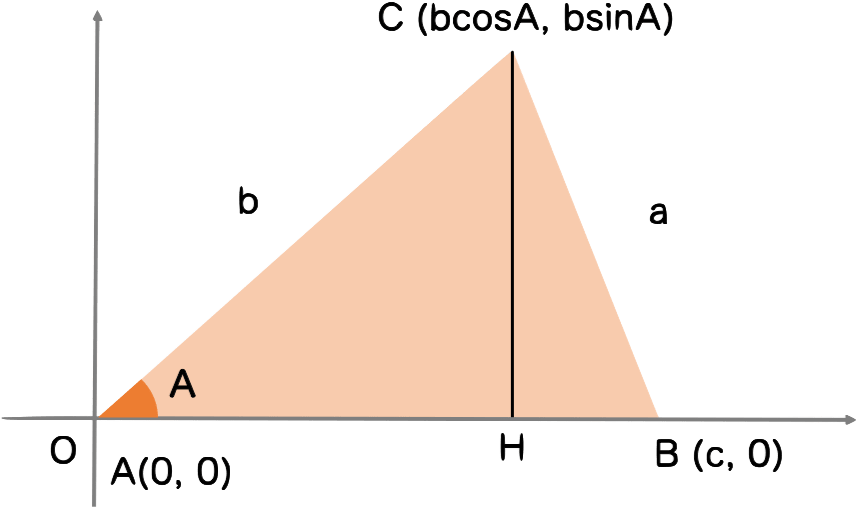
頂点Cから垂線を下ろして、ABとの交点をHとします。三角形CBHにおいて、ピタゴラスの定理を用いると
$$ a^2 = (c-b\cos A)^2 + (b\sin A)^2 $$
となります。
これを変形すると、
$$ a^2 = b^2 + c^2 – 2bc \cos A $$
となります。
ちなみに、これは角度Aが鋭角出会っても鈍角であっても証明ができます。最近の入試では、定理の証明なども出題されるようになってきています。また、定理の証明は本質をつかむことにもつながるのでしっかりみておいてください!
余弦定理を使って何をする?
余弦定理を使って問題を解くのは簡単に2パターンに別れます。それは、2辺と1つの角度がわかっているパターンと、3辺全てがわかっていて、角度を求めるパターンです。
2辺と1つの角度がわかっているパターン
【例題】a=2, b=√3-1, c=120° の時、cの値を求めよ
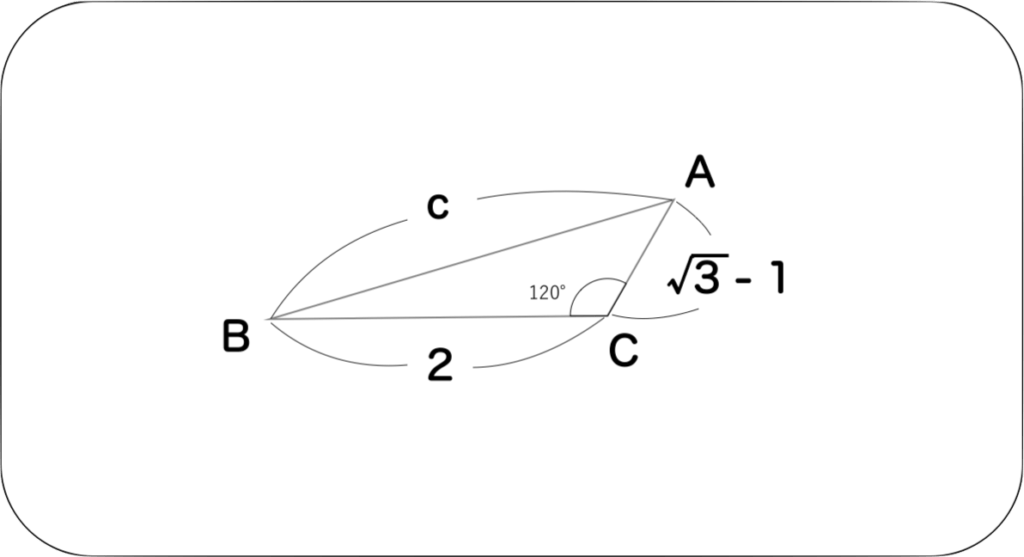
余弦定理により、
$$ c^2 = a^2 + b^2 – 2ab \cos C $$
$$= 2^2 + (\sqrt{3} -1)^2 – 2・2(\sqrt{3}-1) – \frac{1}{2} $$
$$= 6 $$
よって、$c = \sqrt{6} $
3辺全てがわかっていて、角度を求めるパターン
【例題】 三角形ABCにおいて、a=√6, b=2, c=1+√3 の時、Aの値を求めよ
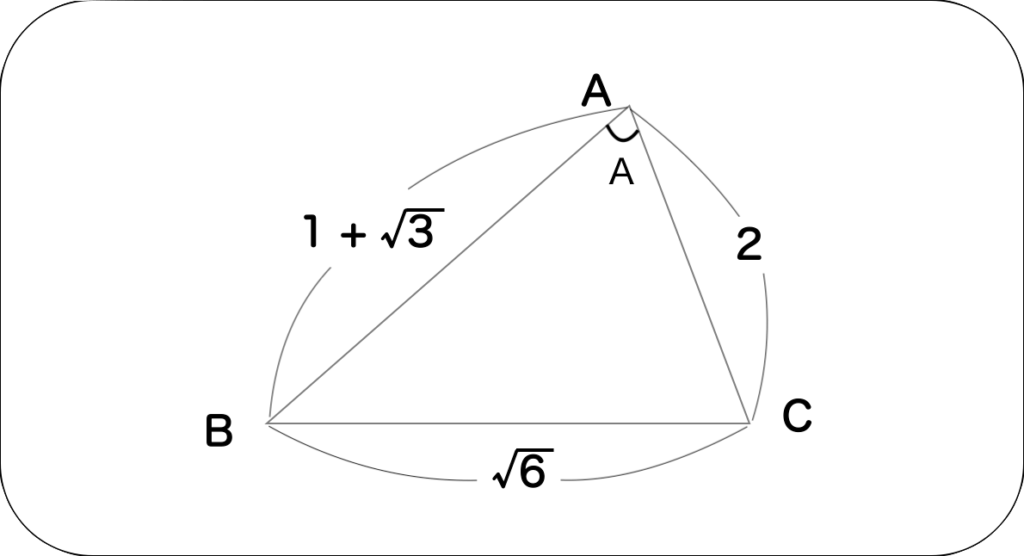
余弦定理により、
$$ \cos A = \frac {b^2 + c^2 – a^2}{2bc} $$
$$= \frac {2^2 + (1+\sqrt{3})^2 – (\sqrt{6})^2}{2\cdot 2 \cdot (1+\sqrt{3}) } $$
$$= \frac{1}{2} $$
よって、A = 60°
これ以外にも、余弦定理を使う問題はありますが、基本的にはこの2パターンを使っています。また、cos を使った式変形においても度々出てくるので、その辺りは問題を解きつつ慣れていくといいと思います。
余弦定理と正弦定理の違いは?
正弦定理は、
$$ \frac{a}{sinA} = \frac{b}{sinB} = \frac{c}{sinC} = 2R $$
と表されます。ちなみに、Rは外接円の半径です。
正弦定理と余弦定理の違いは、単純にsin とcos が出てくるというのが一番です。sin, cos のどちらを使うかによって使い分けるといいでしょう。
また、正弦定理には外接円の半径が出てくるので、外接円が出てきたら正弦定理を使うといいでしょう。
最後に
余弦定理の公式や使い方をイラスト付きで詳しく解説してきました。
ただ単に公式を覚えるだけでなく、自分で導くことができるようになっておくといいでしょう。また、「何を使ったらいいの?」となることがあるので問題を重ねておくと対応力が上がっていきます。
また、余弦定理だけでなく正弦定理もまとめて覚えておくと図形問題を得意にすることができます。三角関数にまつわる他の記事も、ぜひ読んでみてください!