数学はほとんどの問題が「知らないと解けない」ということはありません。しかし、「知っていたら問題が早く解ける」ということはよくあります。
メネラウスの定理はその代表的な例です。これを使えば、5分以上時間を短縮することもできます。
この記事では、そんなメネラウスの定理とは何かということから、メネラウスの証明や実際の使い方などを詳しく解説していきます。
テストの貴重な時間を無駄にしないためにも、ぜひメネラウスの定理を使えるようになってみてください!
目次 (クリックでジャンプ)
メネラウスの定理の賛否
メネラウスの定理は、通常は高校に入ってから習います。普通の中学生なら、少なくとも学校では習わないと思います。
有名な公式なのに学校の先生が教えないのは、やはり「メネラウスの定理を使わなくても、基礎がわかっていれば解ける問題が多いから」です。
ですが、僕はたとえ中学生であっても、この公式を使ってもいいと思います。理由は簡単で、メネラウスの定理を知っていると簡単に解けるようになる問題が圧倒的に多いからです。便利なものがあったら使う、というのは至極当たり前のように思います。
一番やってはいけないのは「中途半端に覚える」ことです。あやふやに覚えることほど怖いものはないので、やるならしっかりやりましょう!
メネラウスの定理とは?
メネラウスの定理とは、以下のような図形に対して
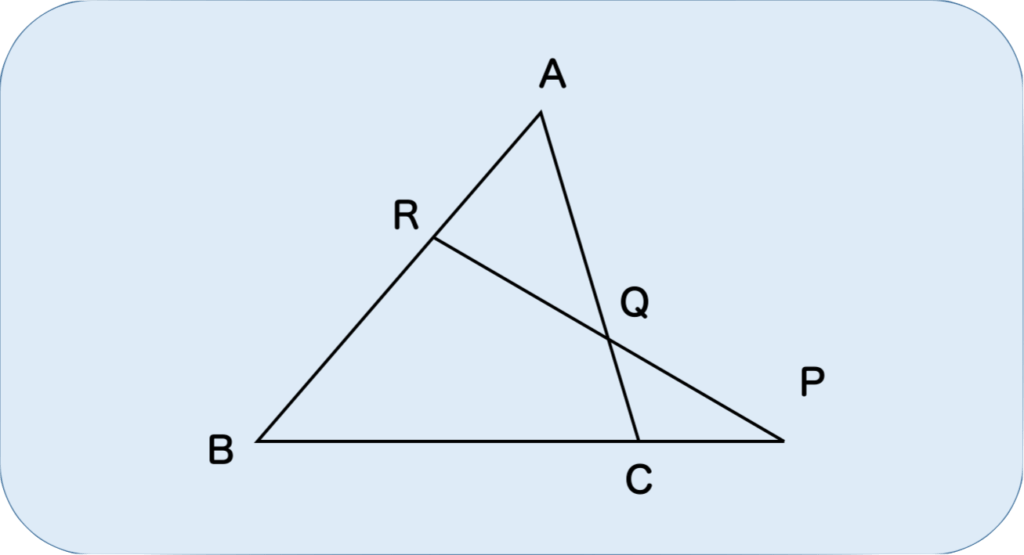
$$\frac{AR}{RB}\times\frac{BP}{PC}\times\frac{CQ}{QA}=1 $$
が成り立つことを言います。
メネラウスの定理を使って何ができるの?
メネラウスの定理を使うと、上の図のようなキツネ型の三角形の長さの比が簡単にわかってしまうのです。
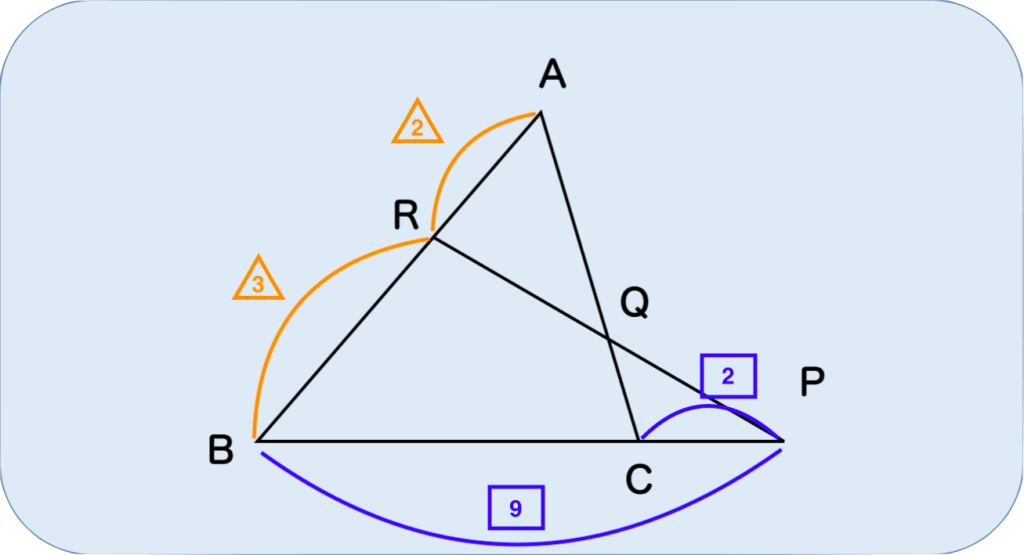
この図を見てください。この図において、もし「AQ : CQ」の比を求めてくださいと言われたらあなたはどうしますか?
普通だと、三角形の相似などを使ってあれこれしますが、時間がかかります。
しかし、メネラウスの定理をうまく使って、先ほどの式に代入してやると
$$\frac{2}{3}\times\frac{9}{2}\times\frac{CQ}{QA}=1 $$
より、「AQ : CQ = 3 : 1」がすぐに求まります。これくらいなら暗算でもできてしまいますね?
このように、メネラウスの定理を使うと、キツネ型の三角形における比を素早く求めることができます。このキツネ型は図形問題に非常に多く出題されるので、覚えておいて損はないと思います!
メネラウスの定理の証明
では、メネラウスの定理をざっくりと証明していきたいと思います。
今回は、一番簡単な面積比を使ってみたいと思います。
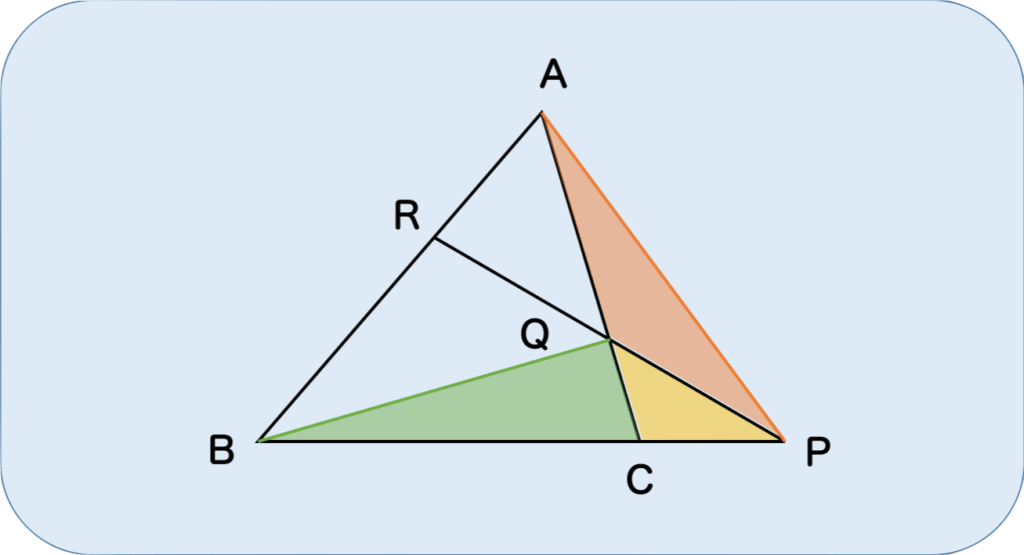
さて、図に何本か直線を引きました。これによって、三角形がたくさんできましたね。
緑色の△の面積をa、黄色の△の面積をb、赤色の△の面積をcとおくと…
まず、緑色の△と黄色の△とに注目します。それぞれの三角形は、高さが等しいので三角形の面積の比はそれぞれの底辺の長さの比になります。よって、
$$\frac{a+b}{b} = \frac{BP}{CP} $$
となります。これより、同様に$\frac{b}{c} = \frac{CQ}{QA} $ となります。
そして、「緑色の△プラス黄色の△」と赤色の△ですが、これはPQが等しいために面積の比は高さの比になります。よって、
$$\frac{c}{a+b} = \frac{AR}{RB} $$
となります。これらすべてを掛け算すると…
$$\frac{c}{a+b}\times\frac{a+b}{b} \times\frac{b}{c} $$
$$= \frac{AR}{RB} \times \frac{BP}{CP} \times\frac{CQ}{QA}=1 $$
となり、メネラウスの定理が証明できました!
なんだかスッキリしないかもしれませんが、メネラウスの証明が問題になることはほとんどありません。なので、「面積の比で証明できる」くらいに覚えておくといいと思います。
メネラウスの定理の覚え方
でも、なんだかメネラウスの定理って、覚えにくいですよね。そこで、よく使われているメネラウスの定理の覚え方を紹介します。
メネラウスの定理では、分母と分子がごっちゃになりがちです。そこで、下の図を見てください。
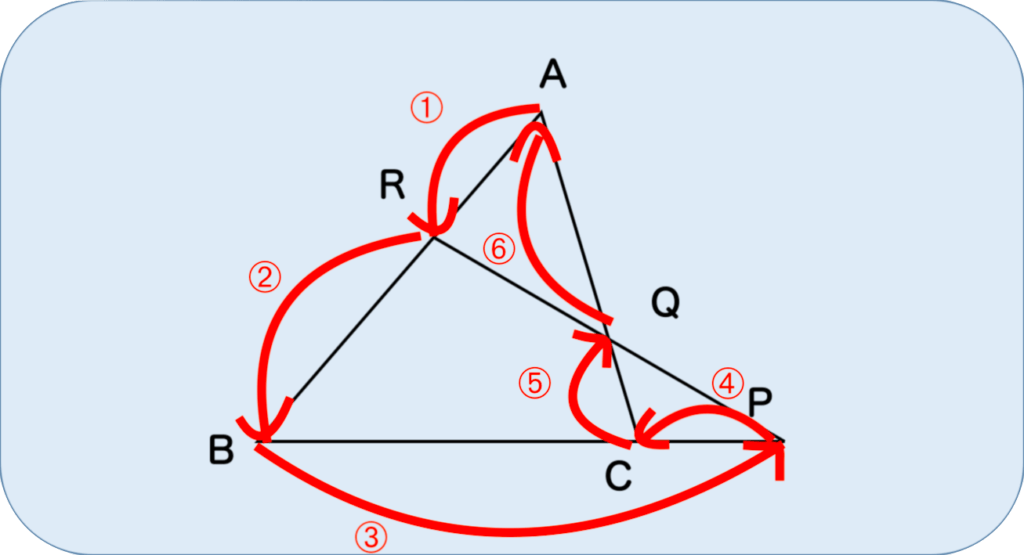
図のように、キツネ型の耳から初めて、一筆書きでまた耳に戻ってくるように番号を振ります。そして、番号の順に分子→分母→分子…と繰り返すと…
$$\frac{➀}{➁}\times\frac{➂}{➃}\times\frac{➄}{➅} = 1$$
となります。これは覚えやすいですね?
ちなみに、メネラウスの定理はキツネ型ならどこからでも始めることができます。例えば、Pから始めるとしたら、次のような感じです。
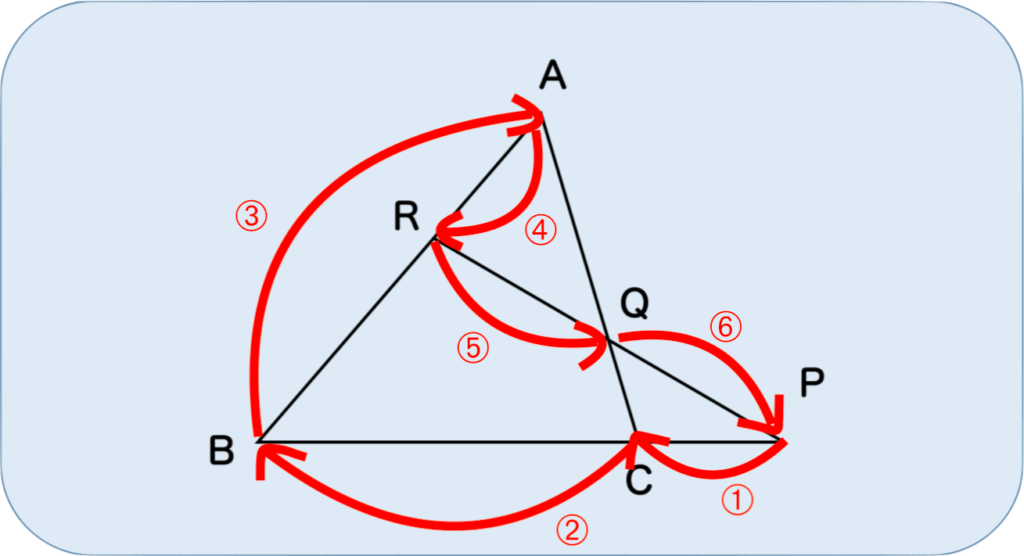
この例だと、
$$\frac{PC}{CB}\times\frac{BA}{AR}\times\frac{RQ}{QP}=1 $$
となります。
このように、反対の耳から反対周りにやることもできます。
ちなみに、最後は結局1になるので、➀を分母から初めて分母→分子→分母… としても、逆にしても結果は同じです。間違えやすいので自分でどちらから始めるか決めておくといいですよ!
メネラウスの定理の逆
あまり登場するシーンは多くないですが、メネラウスの定理の逆についても紹介しておきます。
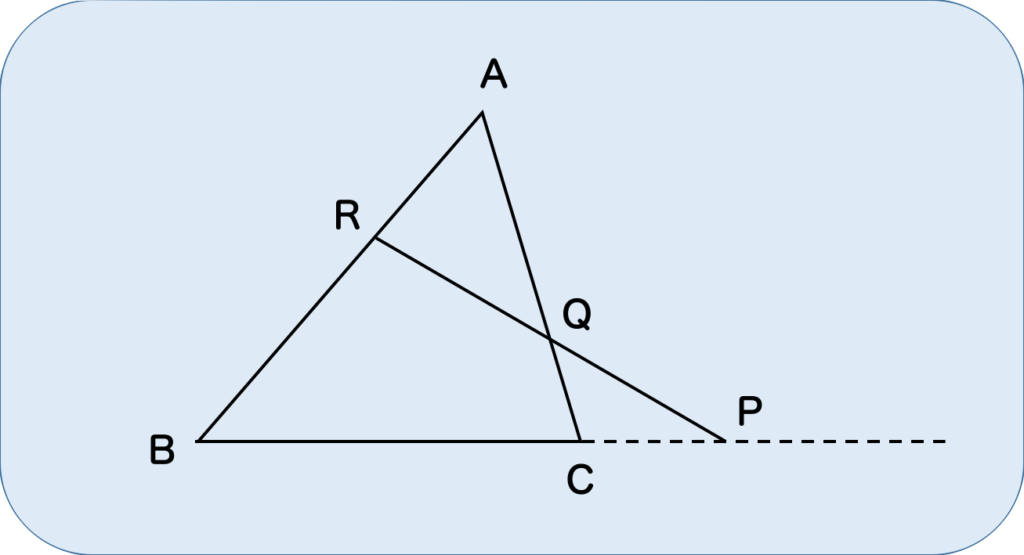
上のような図において、
$$\frac{AR}{RB}\times\frac{BP}{PC}\times\frac{CQ}{QA}=1 $$
が成り立つならば、BCPは一直線上にある。
つまり、メネラウスの定理とは逆で、もし式の積が1になるなら、キツネ型だと言えるわけです。
メネラウスの定理を使った問題
では、早速メネラウスの定理を使った問題を一つ。
下の図において、BQ : QS の比を求めてください。
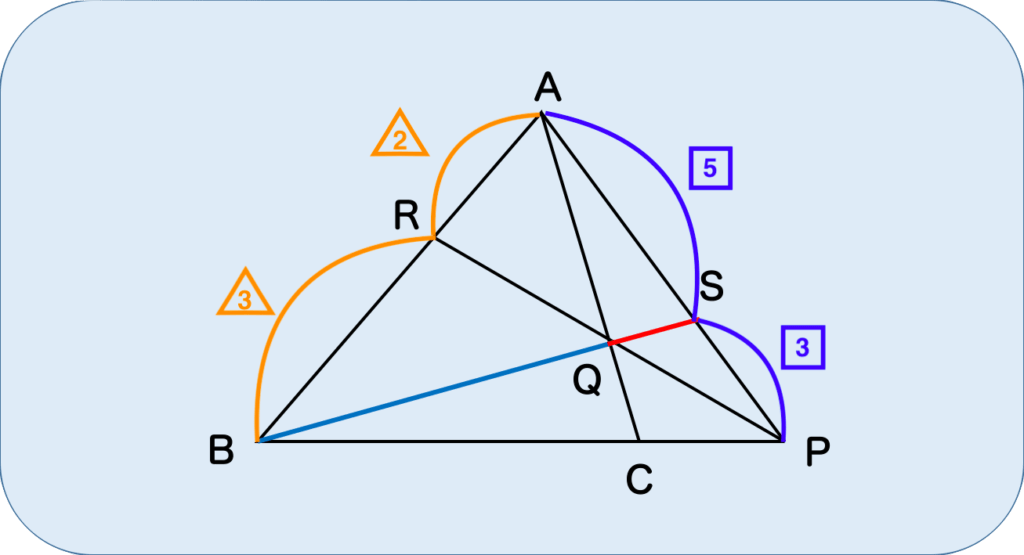
さっきと形が少し違います。
ヒントとしては、どこにキツネ型があるかということに注意してみてください。
解説
正解は…
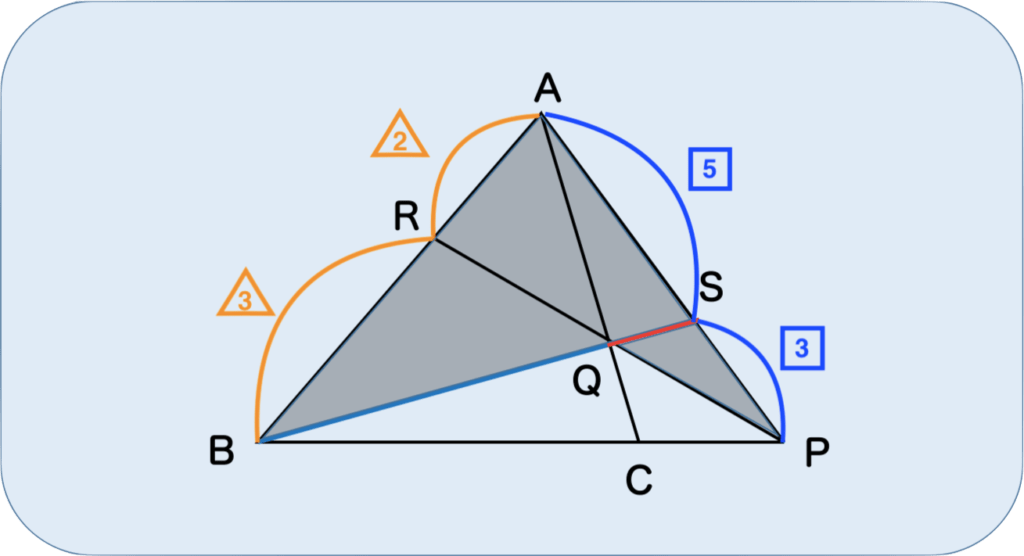
ここにキツネ型がありますね。
なので、左下のBから初めて、
$$\frac{BR}{RA}\times\frac{AP}{PS}\times\frac{SQ}{QB}=1 $$
より、答えは BQ : QS = 4 : 1です。
このように、三角形がたくさんある図形の中にはキツネ型がたくさん隠れています。
最後に
メネラウスの定理ので証明や使い方を説明してきました。理解できたでしょうか?
使いこなせるようになると、圧倒的な時間短縮ができることがわかったと思います。センター試験などのためにぜひ覚えておきたい定理の一つです。
最初にも言った通り、中途半端に覚えるのだけはやめましょう。もし本番に使うつもりなら、演習問題をたくさん積んでおいてください!