第二宇宙速度という速さのことを聞いたことがあるでしょうか?なんとなく、宇宙にまつわる速度というくらいのイメージかもしれませんが、この第二宇宙速度はロケットの問題で頻出なのでぜひ覚えておきたいところ!
そこで、この記事では、第二宇宙速度について、その意味から求め方まで丁寧に解説していきたいと思います。
3分くらいで読めるようになっているので、しっかり読んでみてください!
ちなみに、”第二” というからにはもちろん、第一宇宙速度もあります。詳しくは、こちらの記事をご覧ください!
目次 (クリックでジャンプ)
第二宇宙速度とは?
第二宇宙速度とは、
地球の重力を振り切るために必要な、地表における初速度
のことです。
これだけではわかりにくいかもしれないのでイラストを使って説明していきたいと思います。
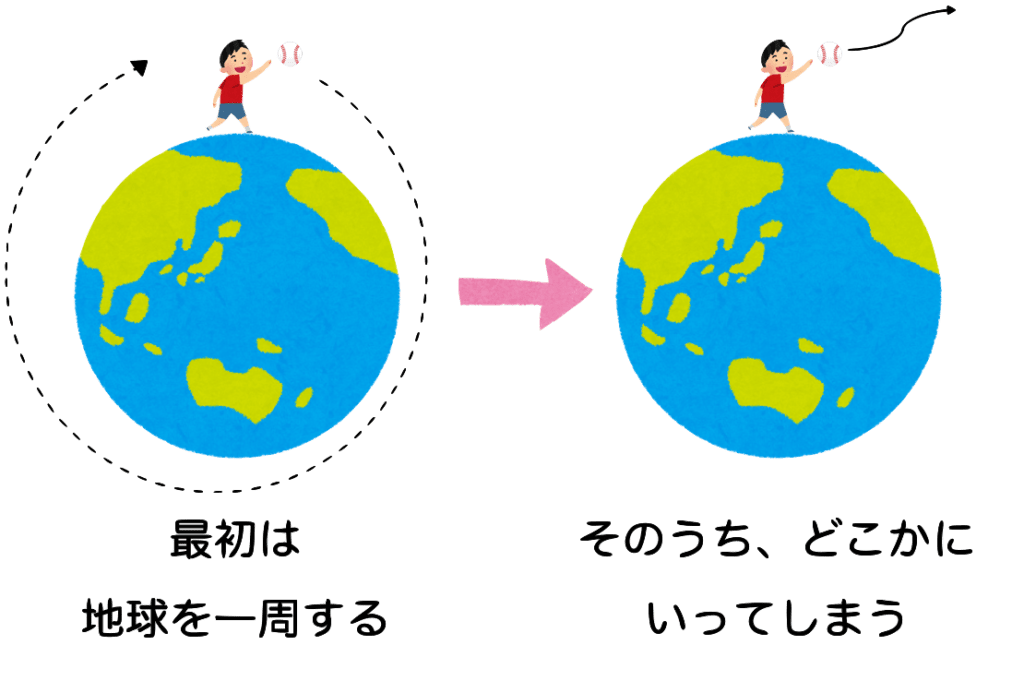
まず、上のイラストのように、めちゃめちゃ早い速度で野球ボールを投げることを想像してみてください。
すると、ボールは地球を回って戻ってきます。
では、もっともっと早い速度ならどうでしょう?頑張ってめちゃめちゃ早い球を投げると… そのうち帰ってこないようになるのは想像できるでしょうか?
この時の速度が、第二宇宙速度です。
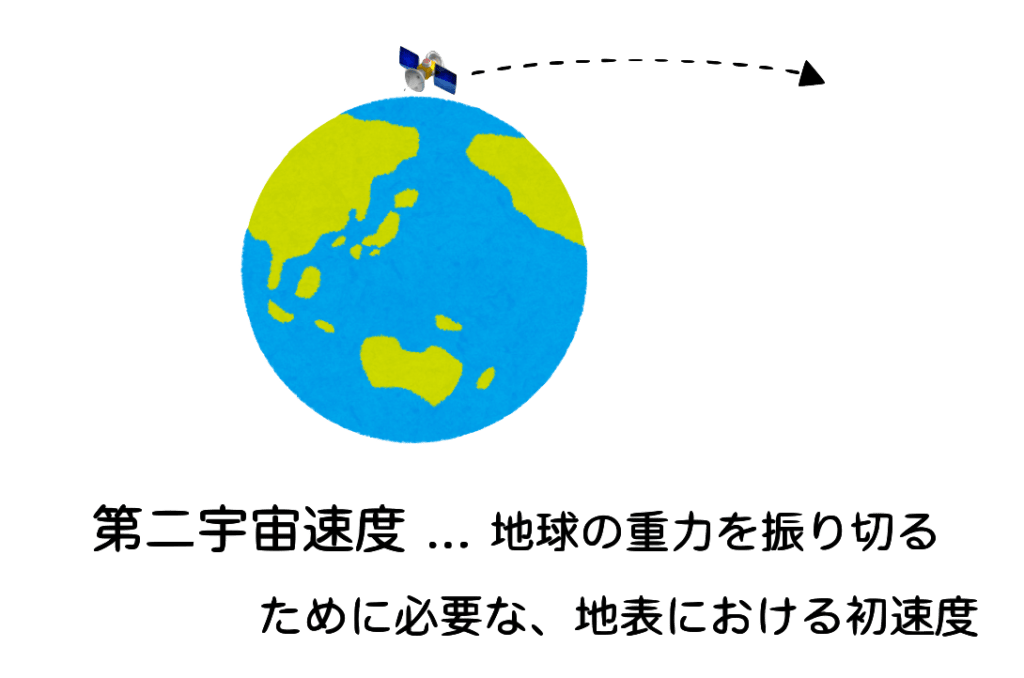
ボールが戻ってくるのは、地球の重力によるものです。この重力を振り切って宇宙に飛び出すことができるのが第二宇宙速度とも言えます。別名の、地球脱出速度という表現の方がしっくりくる人もいるかもしれません。
ちなみに、この第二宇宙速度は地球以外の星においても、引力圏からの脱出速度と考えることもできます。
第二宇宙速度の求め方
では、第二宇宙速度を実際に求めてみましょう。
第一宇宙速度は向心力と引力の釣り合いの式から導出しましたが、第二宇宙速度はそうはいきません。なぜなら、それぞれに働く力が時間と位置によって異なるからです。
では、どうするかというと最初と最後を見てやればいいのです。勘のいい人はピンときたかもしれませんね。そうです、エネルギーの保存則を使います。
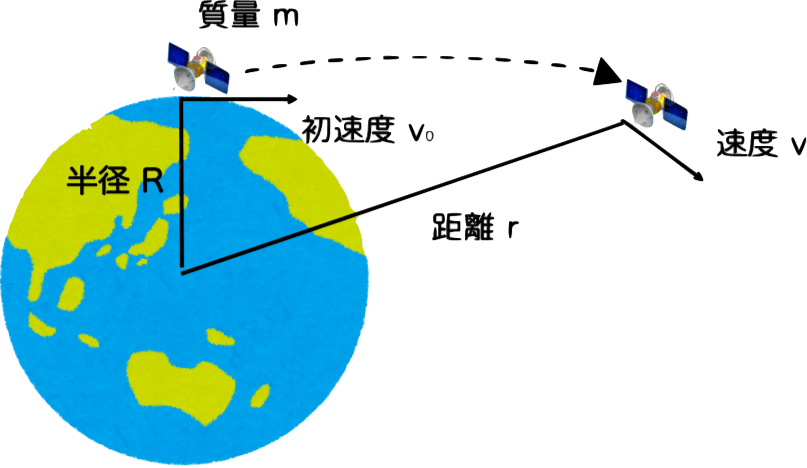
イラストを見てください。このように、半径R、質量Mの地球から質量m、初速度v で人工衛星を打ち上げるとします。この衛星が半径r の位置に来た時について、エネルギー保存則を立ててみましょう。
$$ \frac{mv_0^2}{2} – G \frac{mM}{R} = \frac{mv^2}{2} – G\frac{mM}{r}$$
万有引力の位置エネルギーが $ – G{mM}{r}$ になることに注意してください。
さて、地球の引力を脱出するということは、人工衛星が無限の彼方へ飛んでいくということなので、r → ∞ とすると、
$$ \frac{mv_0^2}{2} – G \frac{mM}{R} = \frac{mv^2}{2}$$
となります。この時、右辺の速度が0以上であれば良いので、$ \sqrt{mv_0^2}{2} – G \sqrt{mM}{R} \geqq 0$ より、
$$ v_0 \geqq \sqrt{2gR}$$
となり、$$ v_0 = \sqrt{2gR}$$ 第二宇宙速度が求められます。
地球の重力加速度g = 9.8 m/s 、半径 R = 6.4 × 10^6 を代入すると、第二宇宙速度は、
$$ v_0 = \sqrt{2gR} = \sqrt(2 \times 9.8 \times 6.4 ≠times10_6 = 11\times 10_3$$
より、約11 km/s と求められます。
見てきたように、第二宇宙速度はエネルギー保存則を使います。第一宇宙速度と合わせると、様々な問題を作ることができるので定期テストや
ちなみに、第二宇宙速度はマッハ 32.6 ですね。音速の約33倍のスピードで出発できれば、地球の引力から逃れることができるのです。
第一宇宙速度との違いは?

第一宇宙速度は、
地表近くを円軌道を描いてまわるだめに必要な、人工衛星の速度の大きさ
のことです。つまり、人工衛星が地球の周りを回る速度です。
この速度は$ \sqrt{gR} $ なので、第二宇宙速度のちょうど$ \\frac{1}{\sqrt{2}} $となっています。
ですが、求め方も異なるので単に「第二宇宙速度 = 第一宇宙速度 × √2」と覚えるのではなく、どちらも最初からしっかりと求められるといいでしょう。
第三宇宙速度について

もしかしたら、第二宇宙速度で地球を脱出した衛星はどの後どこにいくのだろう?と思っている人も多いかもしれません。
実は、第二宇宙速度で地球を離れた衛星は、次は太陽の引力に引っ張られて太陽の周りを回ることになります。
すると、「人口衛星」ではなく「人口惑星」という名前に変わります。ちょうど、地球の衛星が月なのに対し、地球は太陽の惑星という関係に似ています。
ちなみに、この太陽の引力から脱出するために必要な速度を第三宇宙速度と言います。この第三宇宙速度は約16.7 km/s で、なんとマッハ48.6 です。
東京~ロサンゼルスをマッハ50で飛ぶと、なんと8分でついてしまう計算になります。実際にはこの速度を出すのは難しいので、宇宙に飛ばしてからスイングバイなどを利用して加速するのが一般的みたいです。
最後に
以上、第二宇宙速度の意味から求め方まで、解説して来ました。いかがだったでしょうか?
宇宙速度は円運動やエネルギー保存則、さらには運動量保存則など幅広い分野から問題を作ることができるので、狙われやすいところです。
公式を暗記する必要がないですが、保存則からしっかり導くことができるようにしておきましょう。
第一宇宙速度についてわからない人は、こちらの記事も合わせて読んでみてください。