図形の分野でわかりにくい問題の1つに「円周の公式」があります。言葉で言われてもよくわからない部分が多いのではないでしょうか?
そこで、この記事では円周の公式と、その計算例をイラスト付きで詳しく説明していきたいとおもいます。
5分くらいでわかると思うのでていねいに読み進めてみてください!
では、いきましょう!
目次 (クリックでジャンプ)
円周の公式
円の周りの長さを求めるには、次のような公式を使います。
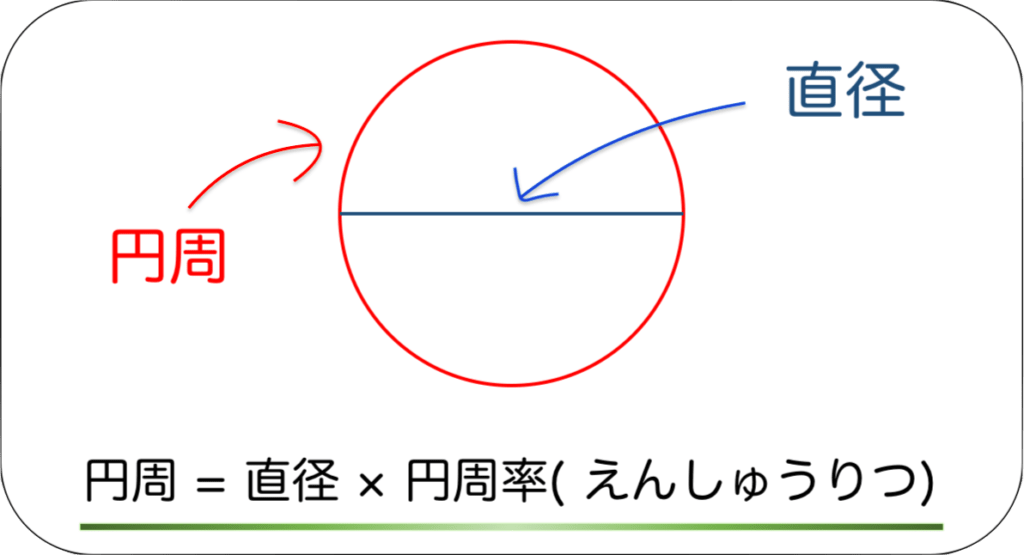
円周 = 直径 × 円周率( えんしゅうりつ)
小学校の算数では、ふつう円周率は3.14を使うと思います。
これだけ簡単な公式だと、覚え方とかを色々使うよりもそのまま覚えた方がいいので、「円周は “直径かける 3.14” 」とストレートに覚えてしまってください!
中学生バージョン
ちなみに、中学生になると円周は違った形の公式で登場します。
それは、円周をl、円の半径をrとすると、
l = 2πr
です。ここでπは円周率になります。
円周率ってなに?
ここで、

という人のために円周率について説明していきたいと思います。
まず、円周をハサミで切って直線にします。そして、それを直径と比べてみると…


つまり、円周率というのは簡単でその名の通り直径と円周の比のことを言っているにすぎません。図でいうと、円周(赤い線) は、直径(青い線) に比べて3.1415… 倍になっているということです。
どっちがどっち… と覚えなくても、図を描けば 円周 = 直径 × 3.14… という関係はすぐにわかりますね!逆にはなりません。
では、なぜ3.14倍なのかというと…

というほかありません。あんまり深い意味はないんですね。
ちなみに、円周率は3.141592… と永遠に続いていきます。だから、中学生はこれをπという記号でおくことにしたのです。
この円周率は不思議な数字で、長年に渡って多くの数学者を惹きつけてきた数字です。また、東大の入試問題にもなっていたりするので興味のある人はぜひ!
円周の公式 ふたたび
では、円周率の意味がわかったところでもう一回、円周の公式を思い出してみましょう。
円周 = 直径 × 円周率
で、円周率ってなんだったかといえば、円周と直径の比でした。つまり、円周率に直径をかければそのまんま円周になるってことです。

要は…
$円周率 = \frac{円周}{直径}$だから、これを変形して $円周 = 直径 \times 円周率$ ってなるわけ。
公式そのまんまですよね?簡単でしょ?
つまり、ややこしい言い方をすれば「円周を直径から出すために用意した数字が円周率だ」ってことです。
んー、わからなかったら飛ばして問題にいっちゃってください!
円周の計算例
では、公式がわかったところで円周の計算問題をいくつか解いてみることにしましょう。
半径が5cm の円の円周を求めなさい

1つ注意しなければいけないのが、「直径を使うか半径を使うか」をごちゃごちゃにしないことです。
つまり、今回の問題でいえば半径が5cm ということは円の直径は10cm なので、円周は、10 × 3.14 = 31.4 (cm) です。
中学生のように解くなら 2π × 5 = 10π (cm) ですね。
先ほどよりも少しひねった問題ですが、これも公式を覚えていれば大丈夫でしょう。
円周 = 直径 × 円周率 なので、直径 = 円周 ÷ 円周率です。
よって、12.56 ÷ 3.14 = 4 (cm) が円の直径となります。
まとめ
円周の求めかたについて説明してきました。
まとめると、
円周は直径 × 3.14(円周率) で求められる
円周率っていうのは、直径に比べて円周がどのくらい長いのかを表す
ということでした。
最後に
円周の求め方の公式と計算例を解説してきました。しっかりと理解することはできたでしょうか?
円周率のところで “?” となる人も多いかもしれませんが、定義さえしっかりと理解してしまえばどうということもありません。
一度理解してさえしまえば、あとやることは「例題を解いて、知識を定着させる」ことです。しっかりと問題集などで確認してみてください!