三角関数の中で、余弦定理と並んで重要なのが正弦定理です。定期テストや毎年のセンター試験などでは見ない年はないと言っていいというくらい出題されています。
しかし、余弦定理に比べると頻出度が低いためか、ついつい忘れがちになってしまうのが正弦定理です。頭からポーンと飛んでしまったりして、めちゃめちゃ焦ります。
そこで、この記事では正弦定理の証明から問題の解き方まで京大生ブロガーの僕が徹底解説していきたいと思います。
3分くらいでわかるようになっているので最初から最後までじっくりと読んでみてください!
目次 (クリックでジャンプ)
公式として覚えておきたいカタチ
正弦定理とは、下の図のような三角形において
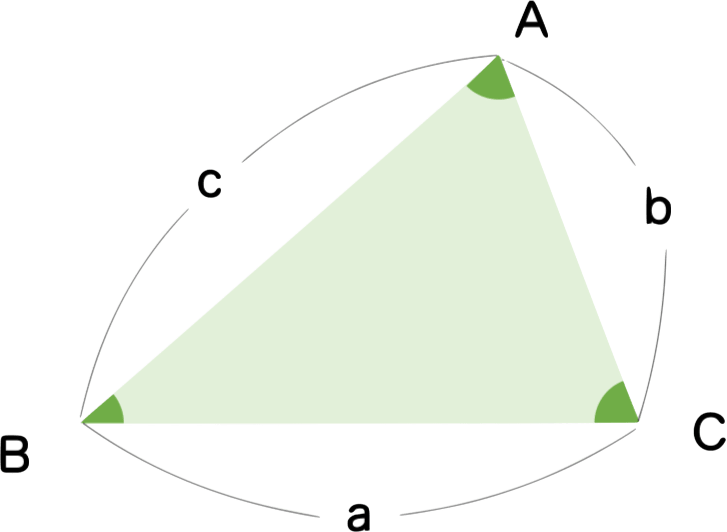
$$ \frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C} = 2R $$
ただし、Rは△ABCの外接円の半径
が成り立つことを言います。
たまに、最初の方だけを覚えている人もいますが、外接円の半径が出てきたりする問題も結構あります。なので、最後の2Rまでしっかり覚えておいてください!
正弦定理の証明
証明問題として出題されることはそこまでないので、理解度を優先してざっくりと証明していきたいと思います。
まず、下のような三角形ABCを用意します。そして、頂点Aから辺BCに下ろした垂線の足をHとします。
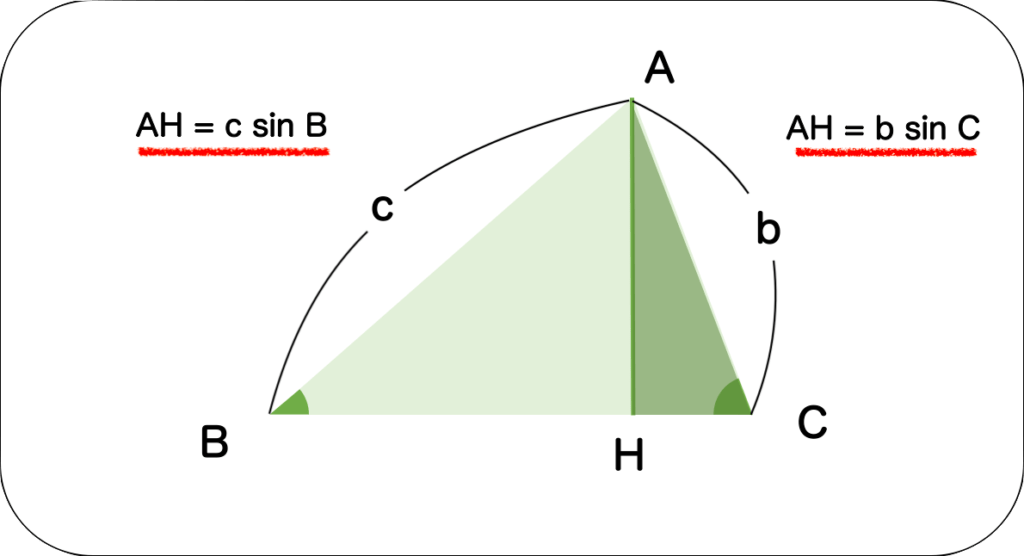
この時、△ACD と△BCDから、AHにおいて2つの式が成り立ちます。
$$ AH = b\sin C \tag{1}$$
$$ AH = c\sin B \tag{2}$$
(1)、(2) より、
$$ b\sin C = c\sin B $$
よって、$ \frac{b}{\sin B} = \frac{c}{\sin C }$が成り立ちます。
同様に、頂点BからACに垂線を下ろすと、$ \frac{a}{\sin A} = \frac{c}{\sin C }$ を得ることができます。
よって、$ \frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C} \tag{※}$ が成り立ちます。ぜひ確認してみてください。
三角形の面積の公式を使った証明
ちょっとズルですが、三角形の面積の公式を覚えている人はこんな解き方もできます。三角形の面積の公式は、
$$ S = \frac{1}{2} ab \sin C = \frac{1}{2} bc \sin A \tag{3}$$
ですよね?(1つ省略しましたが…)
ここで、(4)式の両辺をbで割ってやり、移項して整理してやると
$$ S = \frac{a}{\sin A} = \frac{c}{\sin C}$$
を簡単に導くことができます。これは、実は先ほどのと変わらないのですが、「こんな解き方もあるんだなぁ」くらいに思っておけばいいと思います。
さて、ここからが本題です。公式の中に外接円が出てきているので、外接円を書いてみましょう。
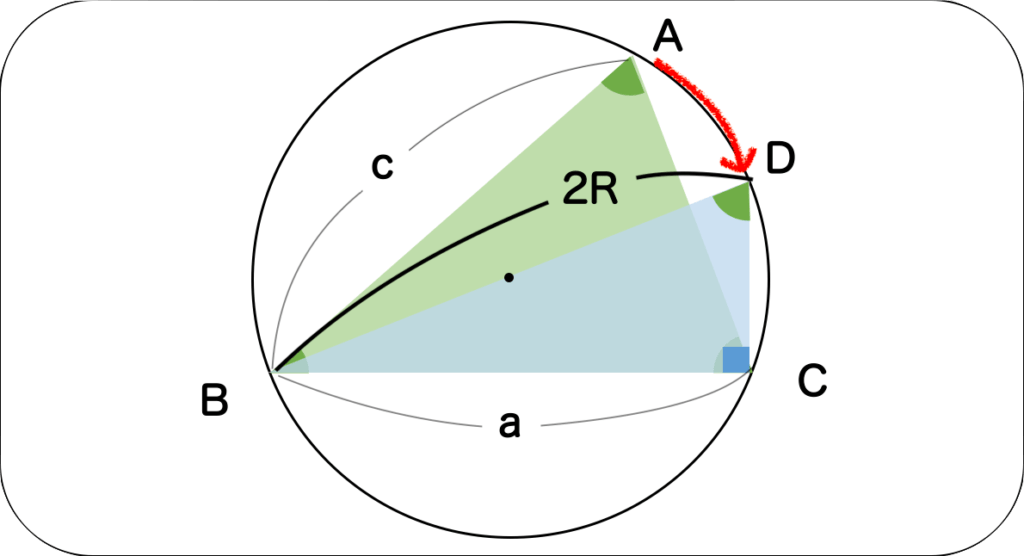
角Aに注目してください。当然ですが、外接円の上にありますよね?
これを、ズズズッと角Cが直角になるまで持ってきます。こうすると、この時は先ほど証明した余弦定理もどきを使って同じように、
$$ a\sin D = BD\sin \frac{\pi}{2} \tag{4}$$
が成り立つのはいいでしょうか?この時、円周角は等しいので、$\sin A = \sin D$、また、$ BD = 2R$ 、$\sin \frac{\pi}{2} $、なので、(3)式を整理すると、
$$ a\sin A = 2R$$
となります。これより、これを(※)に代入すると、正弦定理の公式になります。
ちなみに、Aが鈍角だった場合には$\sin (\pi – A) = \sin A $ という公式を使って、角Aを鈍角の側に戻すだけです。
このように、”正弦” 定理なのだから正弦(sin)が出てくるだろう、そして公式に外接円が出てくるので、とりあえず外接円を書いてみよう、とすれば証明の細かいところまで覚えておかなくて済みます。
これは、正弦定理に限らず証明問題全般に言えることなので、ぜひ覚えておいてください!
正弦定理を使った問題の解き方
では、正弦定理はどんな問題において役に立つのでしょうか?それは、ズバリ「三角形において、角と対辺のペアを求める問題」と「外接円を使った問題」です。
三角形において、角と対辺のペアを求める問題
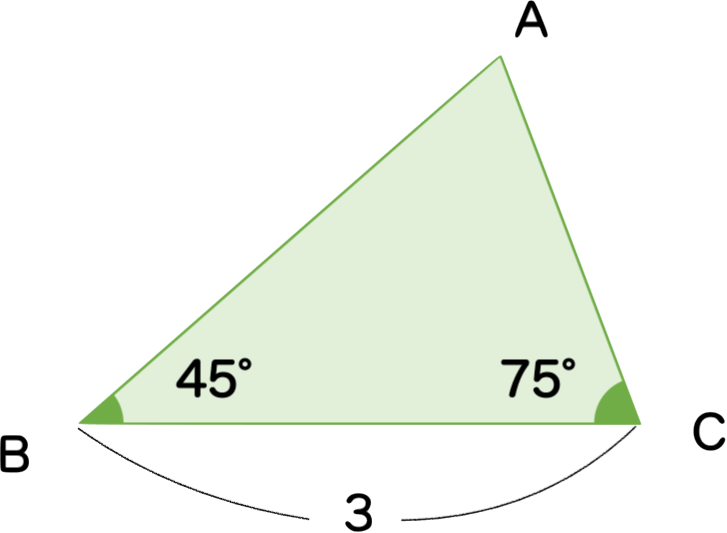
例題 三角形ABCにおいて、a=3、B = 45°、C = 75°のとき、bの値を求めよ
$$A = 180° – (45° + 75°) = 60°$$
正弦定理により、$\frac{a}{\sin A} = \frac{b}{\sin B}$
よって、$b = \frac{\sin B}{\sin A} \cdot a $
$$b = \frac{\frac{1}{\sqrt{2}}} {\frac{\sqrt{3}}{2}} \cdot 3 = \sqrt{6} $$
正弦定理を知らないと補助線などが必要になりますが、この正弦定理を使うと一発でポーンと答えが出てしまいます。
外接円を使った問題
例題 上の問題の三角形において、外接円の半径を求めよ
これは簡単ですね。
$$2R = \frac{a}{\sin A} $$
より、$ R = \frac{3}{2 \cdot \sin 60°} = \sqrt{3} $です。
ここで注意したいのが、Rを直径と半径のどっちかをしっかり意識しておくことです。Rが大文字なので、たまに直径だと思ってしまう人がいるのです。
もし問題を解いていて迷ったら、実際に図を書いてみるといいと思います。そうすると、Rが直径か半径かはほぼ100%の確率で当てることができます。
そのくらいざっくりと覚えておくので問題ないと思います。
もちろん、テストではここで出題した問題のように簡単に正弦定理が使えるとわかるわけではありません。しかし、基本的にはこのパターンさえ覚えておけば現場でなんとかなると思います。
基本がわかったら、あとは問題を解いてどのような問題があるかをしっかり頭に叩き込んでおけば大丈夫でしょう。
最後に
正弦定理の証明から問題の解き方までを解説してきました。証明問題が多少ややこしいですが、しっかりと理解できたでしょうか?
最初にも言った通り、ほとんどの問題が余弦定理を使って解くことができるので忘れてしまいがちですが、いざという時のために頭に入れておくことが重要です。
基本原理さえ覚えてしまえば、あとは問題を解いていくだけなので、しっかりと練習問題を解いていくといいでしょう。
余弦定理が怪しい人は、こちらの記事も合わせて読んでみてください!
また、数学の問題は実際に演習問題で回数をこなさないとテストで実力を発揮することはできません。そのためにも、早いうちから演習問題を解いていった方がいいと思います!