学校でデータの扱いについて勉強した人も多いかもしれませんが、一度聞いてもよくわからないことって多いですよね?
特に、中央値(メジアン)や最頻値(モード)については数IIBで初めて知ったという人も多く、馴染みのない言葉だと思います。
そこで、この記事では平均値・中央値・最頻値の3つについて、求め方や計算方法などをそれぞれ解説していきたいと思います。
3分ほどでわかりやすく説明していくのでじっくりと読んでみてください!
目次 (クリックでジャンプ)
基礎知識
調査や実験などで得られた測定値の集まりをデータと言います。そして、そのデータの中心的な傾向を示す値を代表値といいます。
なので、この代表値というのは「データがだいたいどのような傾向を示すか」をざっくりと表しているのです。
- データが大体どのような特徴を示しているか?ということを表している値
この代表値の中で、特によく使われているのが平均値、中央値、そして最頻値です。この記事では、これらについて解説していきます。
平均値はわかりやすい
平均値とは?
平均値は、代表値の中で最も有名です。日常生活の中でも使うので平均値についてはよくわかっている人も多いと思います。
平均値はざっくりいうと、各データの値の総和をそのデータの個数で割ったものです。英語ではAvarage(アベレージ)と言います。
正確には、次のように定義されています。
N個の値、$x_1, x_2, x_3, … x_N$からなるデータに対し、それらの総和をNで割ったものをこのデータの平均値と言い、$\overline{x}$で表します。
$$\overline{x} = \frac{1}{N} (x_1+x_2+x_3+… +x_N)$$
これだけ見せられても、わかりにくいですよね。実際の例を使って求めてみましょう。
平均値の求め方
10個の値 2, 3, 3, 4, 4, 5, 7, 7, 7, 8からなるデータについて、そのデータの平均値を求めよ。
平均値は、$\overline{x} = \frac{1}{10} (2+3+3+4+4+5+7+7+7+8) = 5$より求まります。
平均値についてはかなりとっかかりやすいと思うのでサクサク進みます!
平均値のメリット、デメリット
平均値のメリットとしては、すべての値が反映されるということです。すべての値の総和なので、全体的な傾向を見るのにもってこいなのです。
逆に、デメリットとしては、極端に外れた値があった場合にはそれに強く影響を受けてしまうことにあります。
例えば、100人の村があったとして、1人の年収が10億円、他の人は100万円であった場合、その村の平均年収は1,099万円になります。つまり、99人の人が100万円の村でも平均年収が1,000万円を超えることになってしまいます。
このように、極端に変な値があると機能しなくなるのが平均値です。このような理由から、代表値には平均値の他にも中央値や最頻値という値が使われているのです。
中央値とは、真ん中の値のこと

中央値とは?
中央値とは、その名の通りデータを小さい順に並べた時、ちょうど中央にある値のことです。
中央値は、平均値と違って極端な値に対して影響を受けづらいというメリットがあります。
ちなみに、英語ではメジアンと呼ばれ、別の統計用語では50パーセンタイルや第2四分位数と同義となっています。
中央値の求め方
中央値は、データの個数が奇数か偶数かで変わってきます。
データが奇数であれば、中央値はちょうど真ん中の値です。この時はぴったりと決まります。
一方、データが偶数であれば真ん中と呼べるようなデータがちょうど2個あることになります。この時は、これらの平均をとって中央値と呼ぶことにしています。
例題いきましょう。
10個の値 2, 3, 3, 4, 4, 5, 7, 7, 7, 8からなるデータについて、そのデータの中央値を求めよ。
データは偶数なので、4と5の間をとって4.5が中央値となります。
例題のデータは小さい順に並んでいますが、これがごっちゃごちゃの時は小さい順に並べ替えてください!
中央値のメリット、デメリット
中央値のメリットとしては、先ほども言った通り極端に外れた値の影響をあまり受けづらいのです。
一方で、データの比較にはやや不向きな点があります。つまり、データの全体を考慮した値ではなくなるため、単純な比較にならないことがあるのです。
先ほどの100人の村でいうと、大金持ちが1人や2人くらい入ってきたってどうってことないということです。
最頻値とは、もっともよく出てくる値

最頻値とは?
では、最頻値とはなんでしょうか?
最頻値とは、読んで字のごとく最も頻度の高いデータのことです。英語でいうと、モードと言います。
データが度数分布で与えられる時には、度数の最も大きい階級の値を最頻値とします。
ただし、データの数が少ないと「3回しか出てこないデータが最頻値になってしまう」こともあるので注意が必要です。
最頻値の求め方
最頻値の求め方は一番簡単です。
ズバリ、データの中から一番多いものをピックアップすればいいだけ。
例題いってみましょう。
10個の値 2, 3, 3, 4, 4, 5, 7, 7, 7, 8からなるデータについて、そのデータの最頻値を求めよ。
パッとみて、最も多く登場する値は7ですね!
これをみて、「もしデータの数がめちゃくちゃ大きかったらどうするの?」と思った方もいるかもしれません。そういう時には、プログラムを組んだりして見つけることになります。
テストでは数えられる範囲の問題しか出題されないので安心してください!
最頻値のメリット、デメリット
最頻値のメリットとしては、中央値と同じように外れの値に左右されにくいというのがあります。
例えば、100人の村の例でも、たとえ1人の年収が10億でも100億でも、最頻値には全く関係ありません。
逆にデメリットとしてはデータの値が少なすぎる時にはあまり効果がないことです。
極端な話をいえば、100人の村において、年収が1万円、2万円, … 100万円と一人ずつ違ったとします。この時、もし年収100万円の人が引っ越してくれば、この村の最頻値は100万円ですし、引越してきた人が1万円なら1万円になります。
この例で言えば、平均値と中央値はどちらも大きく変わりません。使い所が大切だといういい例ですね。
平均値・中央値・最頻値の違いを図で見てみよう
最後ですが、平均値と中央値、そして最頻値の違いというものをそれぞれ図で理解して見ましょう。
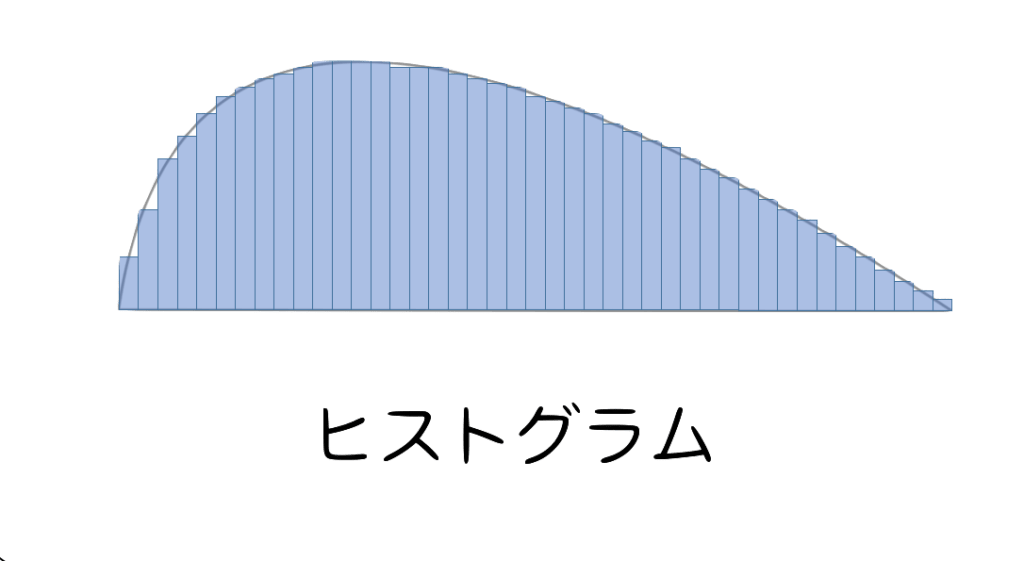
ある集団のヒストグラムが図のようであったとします。
まず、最頻値ですが、これはわかりやすい。最も頻度の高いところなので、山が一番高くなっているところです。このように、ヒストグラムを見たらパッとわかるようになっています。
次に、中央値ですが、これは図のように左右の面積が等しいところが中央値となっています。中央値の厳密な定義は、積分記号を使って表されます。
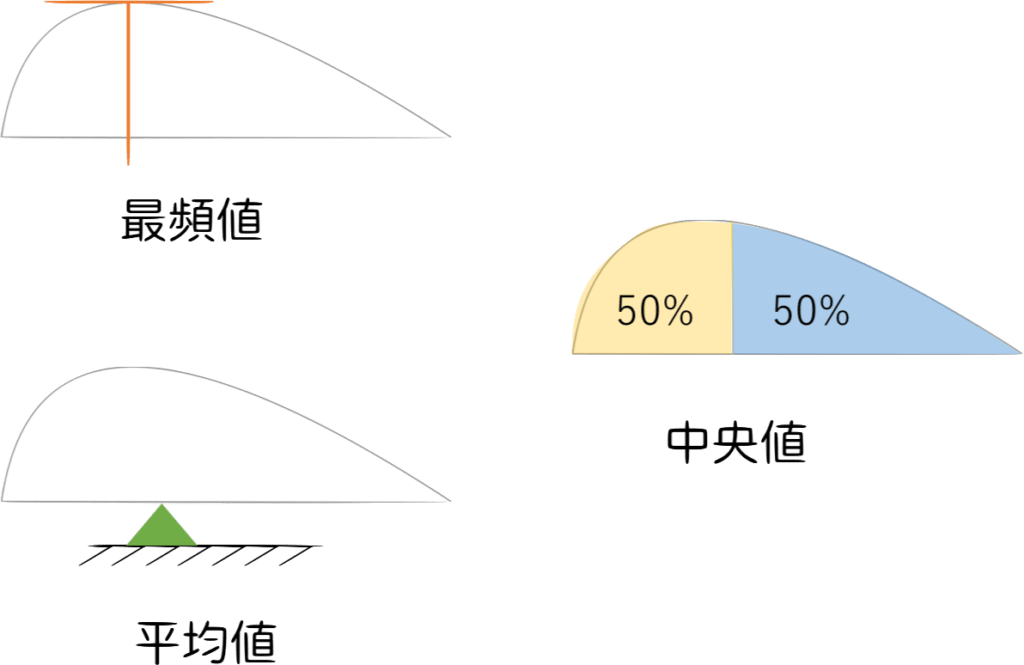
最後に、平均値ですがこれが表しているのは「重心の位置」と言えます。
物理をやっている人にはわかると思いますが、重心というのは、ここを指でおさえるとバランスの取れるポイントになっています。
3つの代表値の使い分け
平均値・中央値・最頻値の3つの代表値にはそれぞれ良い点、悪い点があります。
では、どれを使えば良いかということですが、基本的には平均値を使うと良いと思います。特に、平均値と中央値が大きく乖離していなければこれらの値がグラフを代表していると言えます。
しかし、繰り返しになりますが、代表値は所詮は代表値であってそれ以上のものではありません。つまり、様々なデータを1つの値で表すのには無理があるということです。
なので、一番良い方法としては、ヒストグラムや箱ひげ図などを見て判断をするということです。平均値や最頻値などはそれを端的に表したものだと思っていると大きな間違いをしにくくなるでしょう。
最後に
平均値、中央値、最頻値の求め方や計算方法を紹介してきました。まとめると、
- 平均値…各データの値の総和をそのデータの個数で割ったもの
- 中央値…データを小さい順に並べた時、ちょうど中央にある値のこと
- 最頻値…最も頻度の高いデータのこと
ということでした。
データの代表値についての問題は日常生活にも役に立ちますし、テストでも得点源になりやすいところです。
しっかりと理解をしたら、「チャート式」などを使って、実際に問題を解いて確認をしてみてください!
関連記事:【数学のチャート式】あなたにピッタリの色・難易度を紹介します