学校で数列を習ってから、「シグマ記号の計算は大切だ!」と先生に耳がタコにできるほど言われている人も多いと思います。
しかし、シグマ(Σ)記号を使った計算を苦手としている人は意外と多いのではないでしょうか?
そこで、この記事ではシグマとは何かという基本的なことから、計算方法までを徹底解説していきます。
5分ほどで理解できるように解説していくのでしっかりと読み進めて見てください。
目次 (クリックでジャンプ)
シグマ(Σ)記号の意味

$\sum$とは、ギリシャ文字で「和」という意味です。ラテンアルファベットの ”S” はこのΣに由来するということで、Sum(和)という意味から和の意味として使われるようになっています。
Σを「足し算の公式」だと思っている人も多いかもしれませんが、実はシグマはただの記号です。つまり、$1+2+3+4+ … + (n-1) + n$という数式を$\sum$ を使って表すと
$$1+2+3+4+ … + (n-1) + n = \sum_{k=1}^{n} k $$
のように表す、という意味です。
この考え方を知らないで「Σの公式だ!」という風に思っていると理解するのに時間がかかったりするので注意しておいてください!
シグマ(Σ)記号を使った例
Σ記号では、シグマの下に変数と開始する数、そして上に終了する変数を書きます。(少なくとも、高校までの数学ではそうなっているはずです。)
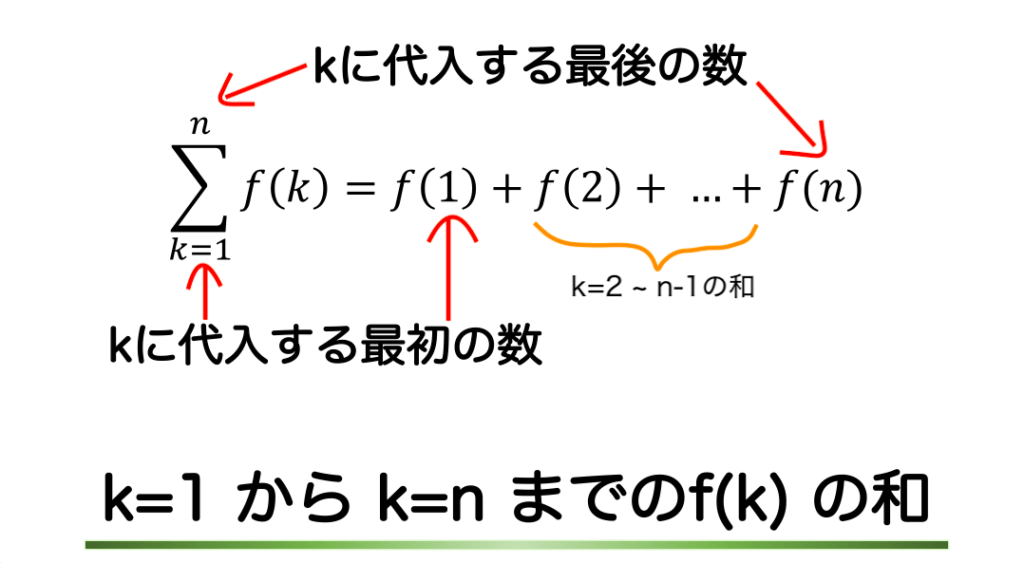
上の式の読み方としては、『変数k を含む数式f(k) において、kを1 からnまで代入した時のf(k)の和』と読むと良いと思います。こうすると式の意味がよくわかるのではないでしょうか?
例としては、
$$\sum_{k=1}^{\infty} 1 = 1+1+1+ … $$
$$\sum_{k=1}^{j-2} k = 1+ 2 + 3+4+ … +(j-2)$$
$$\sum_{k=5}^{n} k^2 =5^2 + 6^2 + 7^2 + … n^2$$
こんな感じですね。では、次の式はわかるでしょうか?
$$\sum_{k=1}^{n} k(k+1) = 1\cdot 2 + 2\cdot 3 + … +n\cdot (n+1)$$
こういう式では、何から始まるかということと、何で終わるかということをしっかり意識するようにしましょう。特に、nなどの文字が出てくると複雑になってくるので間違えることがよくあります。
注意しましょう。
代表的なΣを使った公式
代表的な和の公式を紹介します。どれも覚えておかないと計算にえらく時間がかかってしまうので、暗記は必須だと思ってください。
$$\sum_{k=1}^{n} 1 = n \tag{1}$$
$$\sum_{k=1}^{n} k = \frac{n(n+1)}{2} \tag{2}$$
$$\sum_{k=1}^{n} k^2 = \frac{n(n+1)(2n+1)}{6} \tag{3}$$
$$\sum_{k=1}^{n} k^3 = {\frac{n(n+1)}{2}}^2 \tag{4}$$
$$\sum_{k=1}^{n} ar^{k-1} = \frac{ar^{n-1}}{r -1} \tag{5}$$
中でも、(5)は等比数列の公式と言われています。この記事では、(5)式についてだけ、証明をしておきます。
等比数列の公式
まずは、等比数列について簡単に説明します。
等比数列とは、ある数(初項)に、次々の一定の数(公比)をかけて得られる数列のことです。例えば、初項が2、公比が3である等比数列は
$$2\times 3^0=2, 2\times 3^1=6, 2\times 3^2=18, 2\times 3^3=54, … $$
といった具合です。
初項がa、公比がrである等比数列{$a_n$}の一般項は、
$$a_n = ar^{r-1} $$
です。これらの和を$S_n$とすると、$S_n=a+ar+ar^2+ …ar^{n-1} $となります。
そして、これらの和についてですが…
$$S_n=a+ar+ar^2+ …ar^{n-1}+ … \tag{※}$$
と、この両辺にr をかけたものを作ると
$$ rS_n=ar+ar^2+ar^3 …ar^n+ … \tag{※※}$$
とします。これらを片々引いて(※)- (※※) としてあげると
$$S_n=a+ar+ar^2+ …ar^{n-1} $$
$$ rS_n=ar+ar^2+ar^3 …ar^n$$
より、
$$rS_n – S_n = -a + ar^n $$
となります。これを整理すると、
$$S_n = \frac{a(r^{n -1})}{r-1} $$
となります。この公式の証明は、たまに問題になったりするので覚えておくと良いと思います。
また、他の公式の証明は省略しますが、テストに出てきた場合にはおそらく誘導があるのでそれに従って解いていくと良いと思います。
ほとんど暗記みたいなものなので、覚えてしまうのが手っ取り早いと思います。
数式にもかなり綺麗な法則性があるので覚えやすいと思います。これを覚えることがシグマ記号の問題の第一歩となるのでサクッと覚えてしまいましょう。
シグマを使った計算
シグマを使った計算問題については、基本的なものから応用までたくさんあります。ここでは、基本的な2つの例題を使って「公式をどのように使うか」をチェックしていきたいと思います。
例題1
これは、公式に書いたところの(2)式を使います。つまり、
$$ \sum_{k=1}^{n} k = \frac{n(n+1)}{2} \tag{2}$$
を使って、
$$ \frac{n(n+1)}{2} = \frac {100(100+1)}{2} = 5050$$
となります。
こういった簡単な問題は公式を暗記しているかしていないかを聞いているようなものなので、ちゃっちゃと片付けてしまいましょう。
例題2
少し難しくなりました。和におけるk番目の項はk(n-k+1) と表されるということに気がつくでしょうか?
なので、(与式)$=\sum_{k=1}^{n} k(n-k+1)$ となります。これを解いていくと、
$$\sum_{k=1}^{n} k(n-k+1)$$
$$=\sum_{k=1}^{n} (n+1)k – k^2 $$
$$=(n+1) \sum_{k=1}^{n} k – \sum_{k=1}^{n} k^2 $$
$$ = (n+1)\cdot \frac{n(n+1)}{2} – \frac{n(n+1)(2n+1)}{6}$$
$$ = \frac{n(n+1)(n+2)}{6} $$
このように、式をいろいろ変形して公式の形まで持っていくパターンが多くあります。慣れるには様々なパターンの問題を解いてみるのが早いのでぜひ多くの問題に触れてみてください!
最後に
数列のシグマ(Σ)記号の意味と公式、計算方法などを解説してきました。
和の公式は、Σを使ったものをただ覚えるだけでなく、和の形を意識してみると苦もなく問題を解くことができる場合が多いです。
また、部分分数分解などをして、式を変形したりする問題などが解答までの道のりが見えにくいと思うので、たくさんの問題を解いて解放パターンなどを身につけていくと良いでしょう。
問題集は、初心者ならば教科書レベルを、受験生ならば「数学の参考書まとめ」で紹介した「チャート式」などをやってみると良いでしょう。