有効数字って何？ 計算方法や桁数の求め方を詳しく解説します

高校の化学でやっかいなものの1つに、「有効数字」があります。

よく、こんな出題の形式がありますよね？

僕はこの形式、とってもニガテだったのですが、しっかりと学べば意外と楽なことに気がついて、それからは減点されることもなくなりました。

この記事では、有効数字って何？という話から、有効数字の求め方、計算方法などについて詳しく解説していきたいと思います！

ぜひ参考にしてみて下さい！

有効数字とは、どれだけ信頼できるか、の値

まず、有効数字って何？ということについてざっくりと解説してみたいと思います。

有効数字とは、次のような概念のことです。

ちょっと難しいですね…

例を挙げて説明したいと思います。

突然ですが、あなたの家から学校までの距離はどのくらいでしょうか？

この質問に対して、次のように答えた人がいたとしましょう。

• Aくん「だいたい10kmくらい」
• Bくん「Google 検索などで正確に測って、10.36km 」

では、ここで次の質問です。Aくんの家から学校を通ってBくんの家に行く時の距離は、いくらでしょうか？

これは、本来なら足し算をするだけでいいのですが、ここで困ったことが１つ。それは、Aくんの家から学校までが、“だいたい10km くらい” だということです。

これに対してBくんは正確に10.36 km と答えているので、足してみると

みたいになってしまいます。

もし、だいたい10km が 9.5 km なら 9.5 + 10.36 = 19.86 km になるし、10.5 km なら20.86 km になります。

ここからわかることは、だいたい 10km というアバウトな数字を 10.36 km という正確な値と足してしまうと、せっかくの正確な値に意味がなくなってしまうのです。

つまりはせっかくBくんがGoogle 検索しても、Aくんが大雑把な値を使ってしまうと だいたい20km くらい、という風になってしまいます。

このように、どちらかが “だいたい” の値を使っていると、もう片方の “正確な” 値というのは意味がなくなってしまうのです。

これが、有効数字の基本的な考え方です。

だいたい10 kmと正確に10 kmは違う？

さて、では今度、AくんがGoogle Map を使って、家から学校までの距離がちょうど10km ジャストだとわかったとしましょう。

この時はAくんから学校を通ってBくんの家まで行く距離を出すのは簡単で、単に足せば

となります。

ここで注意したいのが、10km と10.00km は違う、ということです。

詳しいことは後ほど説明しますが、私たちが普段用いている数字でも、似たようなことが起きています。

例えば、だいたい10cm の長さのものを物差しで測った時に、「10.3 cm くらいかな…」となったとしましょう。

でも、考えてみれば正確に10.3 cm ジャストの長さではなくて、10.3055566… cm の長さかもしれませんよね。

でも、だいたい、「この辺りまでは正確に言えるよね」という値を使って生活をしています。

有効数字とは、この「だいたいどのくらいまで確かだよね」という感覚のことで、これを揃えて計算をしないと知らない間に「20.56km + だいたい」みたいに変なことが起きてしまうよ、というものなのです。

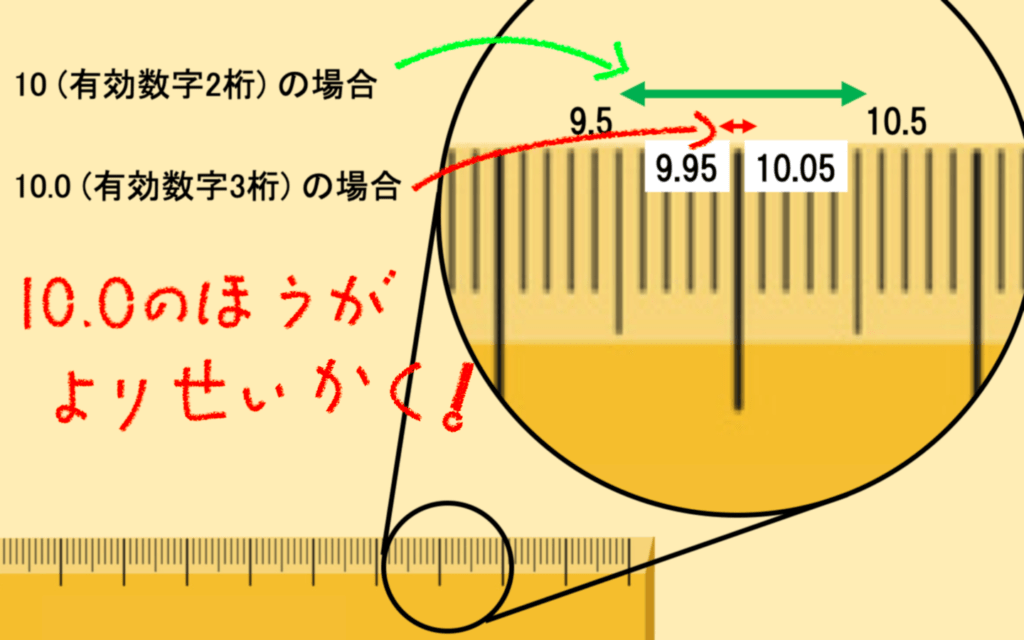
このように、小数点の後に続く0 なども重要になってくるのです。

有効数字の求め方は簡単です

さて、ではいよいよ有効数字の求め方についてです。

先ほども言ったように、有効数字というのは一番上の桁(けた) からいくつまでを有効と見なすか、というものです。

なので、ざっくりとした基準として、正確であればあるほど有効数字は増えるんだ、ということを頭に入れておきながら読んでみると理解しやすいと思います。

0以外で始まる場合は、単純に数字の数

まず、0以外で始まる数字については、単純に 有効数字=数字の数です。

例を挙げて考えていきます。

こんな感じで、小数点以下についてもこの法則は適用されます。

意地悪な問題でもない限りは、これだけ覚えておけば大丈夫です。ただ、テストなどでは次のようなことも聞かれるかもしれないので、覚えておくといいでしょう。

0で始まる場合は、それ以外の数字が出てきてからの数

0で始まる場合は、それ以外の数字が出てきてからカウントをスタートします。

例を見てもらうとわかるのですが、間に0などが入ってもそれはカウントします。

なので、最初に0以外の数字が出たところから、最後にある数字まで正確に数えていってください。

小数点より右側にある0はカウントする

さて、最初の方の話でもありましたが、10 km と 10.00km は有効数字的には全く別の数字です。

この例のように、最後に0があってもしっかりとカウントしてください。

ここまで読んでもらった人はわかると思いますが、10は有効数字 2桁、10.00 は有効数字4桁なので、10.00 の方が信頼できる数字です。

この辺りをしっかりと抑えている人は、単位で不安な点はありませんよ！

$10^4$ などがつく場合はどうなるの？

ちなみに、化学では$1.05 × 10^4$ のように、n乗の形がよく用いられます。

この時は、n乗する前の数字だけに注目するのがコツです。

このように、n乗のところは無視しておいて、今までやってきたように見ればいいだけのことです。

わかってしまえばなんてことないので、しっかりと理解しておいてくださいね！

足し算と引き算は桁数が増えたり減ったりする

注意点としては、足し算や引き算では有効数字が増えたり減ったりすることがある、ということです。

1つ目の例としては、11.0 – 1.7 であれば 9.3 が答えになるのですが、11 は11.0 と違って小数点以下の数字が信用できないため、最終的に小数点を丸めなければなりません。

このため、有効数字2桁同士の答えが、最終的に有効数字1桁になってしまうのです。
(これが31 – 1.7 であれば、答えが29となって、有効数字は変わらず2桁、というわけです。)

逆に、2つ目の例では、有効数字は2桁から3桁に増えています。こちらは、どちらの数字も小数点1桁までは信用できるので、最終的に四捨五入しなくてもよくなるのです。

有効数字の計算方法はどうするの？

さて、それでは有効数字の求め方がわかったところで、次に有効数字の計算方法にいってみましょう。

有効数字の計算も、わかってしまえば「なぁんだ…」となるような当たり前のことなので、チャチャっと進めていきたいと思います！

通常は、受験では有効数字+1 桁をしていればO.K.

さて、いきなり受験ベースのお話ですが、受験では有効数字+1 桁を計算に使って、最後に有効数字を揃えるのがオススメです。

例えば、

というような問題では、

20.3 × 3.31 = 67.193 ≒ 67 (m)

というように、どの数字も有効数字+1 桁にしておいて、最後に有効数字にしてしまうことをおすすめします。

ちなみに、

のように、問題文の有効数字が答えの有効数字より小さい場合は、そのまま計算を進めて、最後に有効数字を2桁にすれば大丈夫です。

ちなみに、余談ですが、有効数字+1 桁で計算をしていても、どうしてもズレてしまうときがあります。

ただ、この方法はほとんどの受験生が使っているために、テストではズレても点数が来ることが多いようです。

特別な指示がなされていなければ、ズレてしまってもしっかりと途中式を書いておけば減点されることはまずないと思いますよ！

有効数字が示されていない場合は、問題文から判断しよう

ちなみに、化学の計算問題などでは有効数字が記載されていないことが多いです。
そういう時は、問題文の有効数字に合わせて答えを書くと良いでしょう。

基本としては、最終的に問題文の一番大きな有効数字に合わせにいけばいいです。

例えば…

という問題では、有効数字の大きな22.4 L に揃える、という感じです。

また、

という問題が出たら、22.4 L の有効数字の “3” をπにも当てはめて、π=3.14 を適用し、3 × 3.14 × 22.4 を計算して、最後に有効数字を “3” になるようにするといい、という感じです。

最後に：心配な人は途中式を書いておけば大丈夫ですよ

以上が、有効数字に関するお話でした。

有効数字で覚えておきたいことをまとめると、以下のようになります。

これさえ覚えておけば、受験では完璧に対応することができます。

有効数字は化学だけではなく、物理や数学などでも問われることが多いので、ぜひ覚えておいてくださいね！