この前、ちょっとした事件がありました。それは…

と中学生に言われたのです。
興味があるのは僕としても嬉しかったのですが、何せ相手は微分、積分はさっぱりわからない中学生。

と思ってググって良記事を探そうとしたのですが、どの記事も淡々とシュレーディンガー方程式を解いていくだけ、という(中学生には) 難しい記事ばかりでした。
そこで、この記事では「中学生」にもわかるように、「数式をなるべく使わず」に、トンネル効果を解説して行きたいと思います。
かなーり簡単にしたので、正確性を欠く部分はありますが、わかりやすさはグッと上がっているので、ぜひじっくりと読んでみてください!
※理系の大学生は読んでも良いケド、参考にしないでくださいネ!
目次 (クリックでジャンプ)
トンネル効果とはどういうものか?
まずざっくりと、「トンネル効果とは何か?」ということについて紹介しますね!
ざっくりと、以下の2つを抑えてもらうと良いと思います!
- 量子力学において現れる物理現象
- ポテンシャルの壁をすり抜ける
コレだけです!
ちょっと難しいと感じる人もいるかもしれないので、それぞれをもう少し説明しますね。
量子力学とは、ミクロの世界の力学(物理)
まず、量子力学とは何か?
非常にミクロな世界では、不思議な物理現象が起きることが知られています。そんなミクロな世界の法則を記述する力学が、量子力学です。
ちなみに、どのくらい小さければいいかというと、めーっちゃ小さくなければいけません。原子とか分子レベルが必要です。
ちなみにちなみに、私たちの生活レベルでの物理を、古典物理と呼んでいます。(ニュートンが体系を完成させたので、ニュートン力学とも)
はい、ここまで読んだ人は「えー、じゃあどっちが正しいの?」と思うかもしれません。
正確には量子力学の方が正しいのですが、私たちの世界のスケールにおいては、同じこと(正確には、ほぼ同じ) なので、簡単な古典力学が使われています。
ポテンシャルの壁とは、坂とか壁のイメージ
次に、ポテンシャルの壁とは何か?ですが、ポテンシャルとは、ざっくりと坂とか壁をイメージしてもらうといいと思います。
正確にいうと、ポテンシャルエネルギーです。つまり、エネルギーの壁、という意味。
そこらへんにある小石をポイっと投げると、当たり前ですが下に落ちますよね?
逆に、下にある石を上に上げようとすると、”エネルギー” を与えてやらなければいけません。
つまり、下から上に行くには、エネルギーの壁を乗り越える必要がある、という訳です。
ここまでくれば、大体のイメージがつかめるので、いよいよトンネル効果のそれっぽい解説に入って行きたいと思います。
最初にも言いましたが、いかんせんざっくりとした解説なので悪しからず。
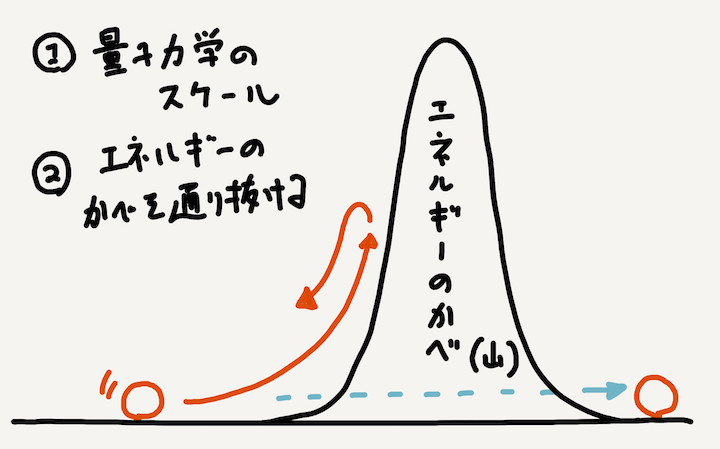
まとめると、以下の図のようになります。

ポテンシャルの壁をすり抜けるとは何か?
さて、ではもう一度下の図を見てください。コレに解説を加えて行きます。

古典力学(私たちの生活レベルのスケール) では、左から転がった玉は、どうなるかというと、坂を途中まで登って跳ね返ります。
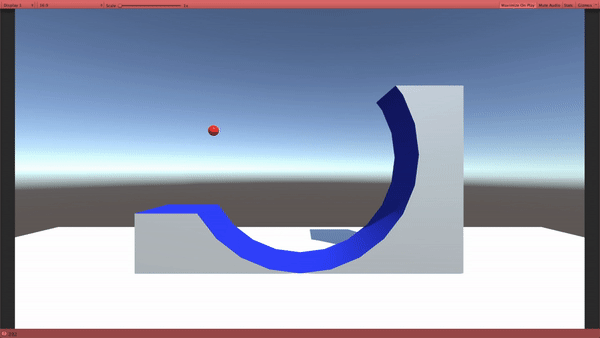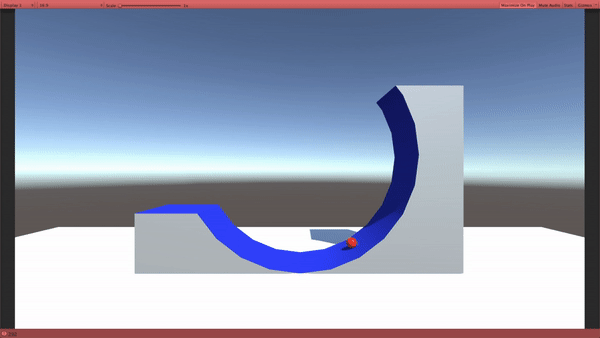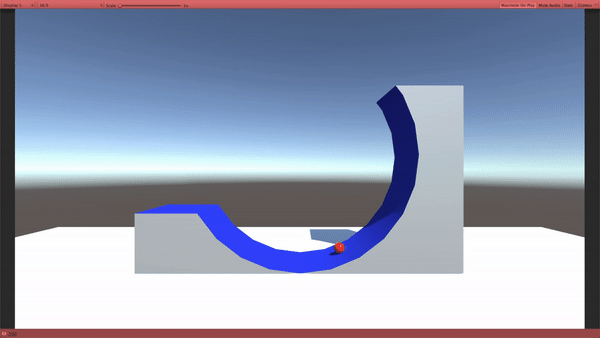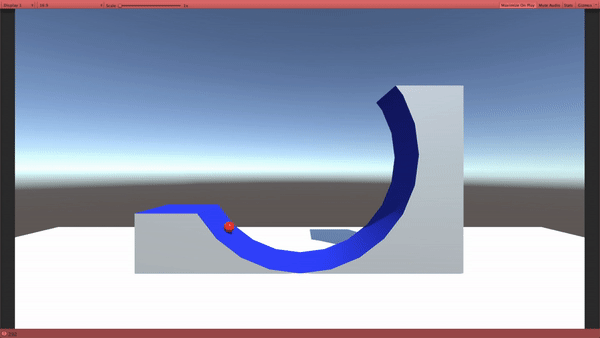

では、量子力学ではどうなるのか?
量子力学では、赤い玉のように、”あたかも壁がないかのようにすり抜ける” ものが出てくるのです。
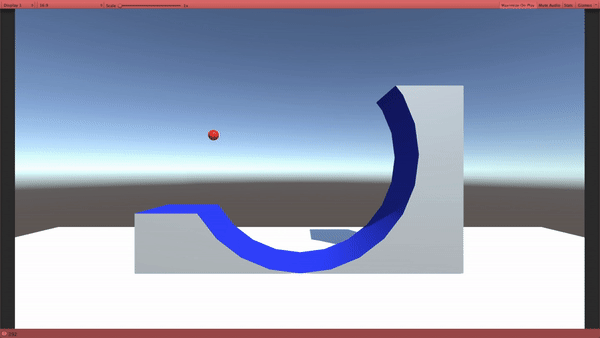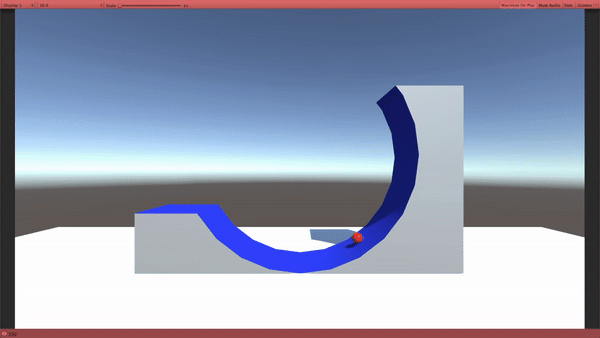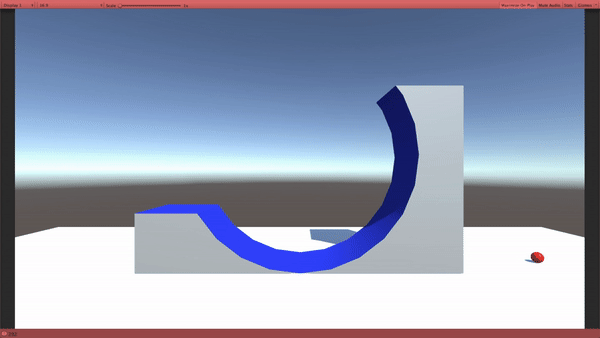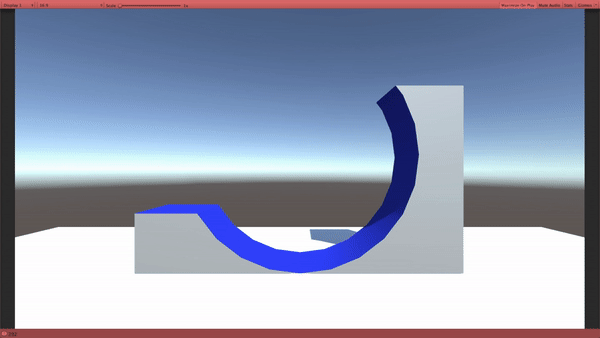

まるで、山にあるトンネルを通って山の向こう側に行ってしまうみたいに見えることから、トンネル効果と名付けられました。
これの何がすごいかというと…
本来は(古典力学では)、坂を登りきるだけのエネルギーを持っていなければ右側に行けないはずの粒子が、小さなエネルギーでも坂を通過してしまう
ということです。
もし、「山を越えられる」エネルギーを持っているものがショートカットをしたのなら、それほど驚くことではないのですが…
でも、トンネル効果はそうではなくて、「(古典力学では) 絶対に右側にいけないはずの粒子が、すり抜けてしまう」という不思議な現象なのです。
トンネル効果の注意点
以上がトンネル効果の説明ですが、これだけだとあまりにもざっくりとしすぎていろんな誤解があるかもしれないので、注意点を軽く述べておきます。
注意点は以下の4つです。
- 非常に小さいスケールで起きる
- 全ての玉(粒子) がすり抜ける訳ではない
- 実際に物理的な壁をすり抜けている訳ではないし、穴が空いている訳でもない
- 同じ粒子がすり抜けているのかわからない
えー、つまりは人がトンネル効果で壁をすり抜けたりはできないし、すり抜けをしたとき、壁は壊れたりしない、ということです。
4番はどういうことかというと、同じ粒子がすり抜けたか、というのはわからないということです。
ポテンシャルの手前の粒子が “消え” て、壁の奥に粒子ができる、というだけで、それが同じものかどうなのか確かめようがない、という感じみたいです。
物理的現象を式なしで追ってみる
以上でざっくりとした説明は終わりなのですが、もう少し説明をしてほしいという要望をいただきました!
そこで、もう少しだけ詳しく説明をしたいと思います。
ちょっと抽象度が上がるので、ふんわりした話に聞こえるかもしれませんがご容赦ください。
では、説明していきたいと思います!
古典力学の場合、どうなるか?
使うのは、以下のような薄いポテンシャル壁です。ポテンシャル壁というのは、単純に “壁” だと思ってもらうといいでしょう。
ここに、(ポテンシャル障壁よりも低いエネルギーを持った) 粒子がやってくるとします。
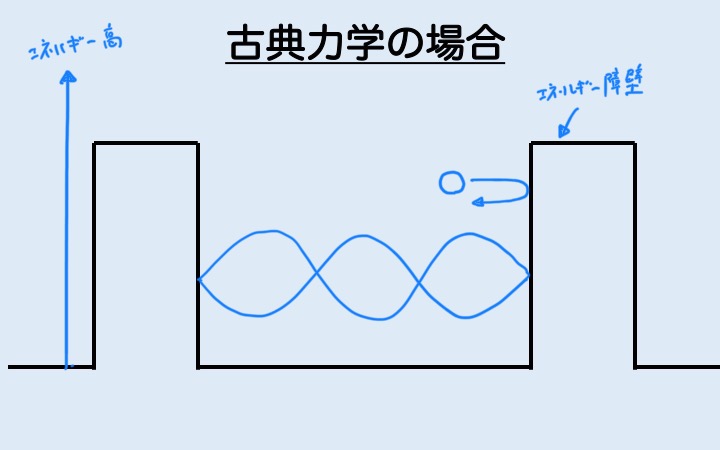
コレが、古典力学(私たちの生活スケール) だとどうなるかというと…
もちろん、壁で跳ね返ります。

この時、跳ね返る位置は、厳密に壁の位置になります。
本当に壁にボールを当てたように、ポヨンと跳ね返ってくるイメージです。
粒子が存在する確率を表すグラフは、以下のようになります。壁の前で0になっているということに注意しておいてください。(当たり前ですが…)
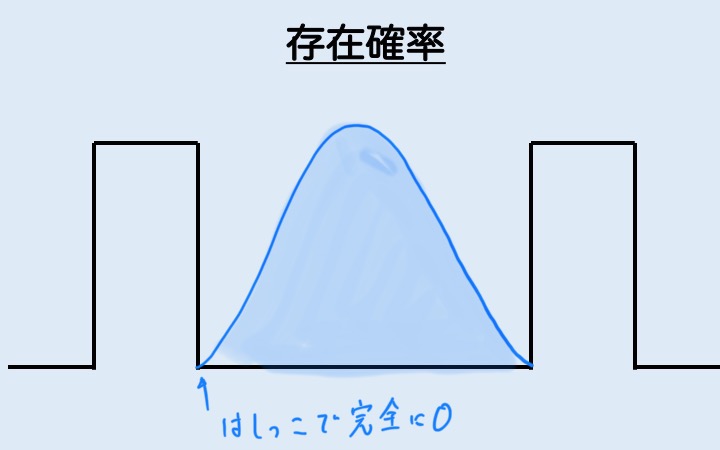
※n=1の場合
ちなみに、真ん中にいる確率が高くなっていますが、これは例えば右→左→右→左と移動した時、
- 右… 2回
- 左… 2回
- 真ん中… 3回
であることからわかると思います!
量子力学の場合は、壁に染み出す
では、量子力学の場合だとどうか…
まずは、そこそこの厚みを持っている壁の場合についてです。
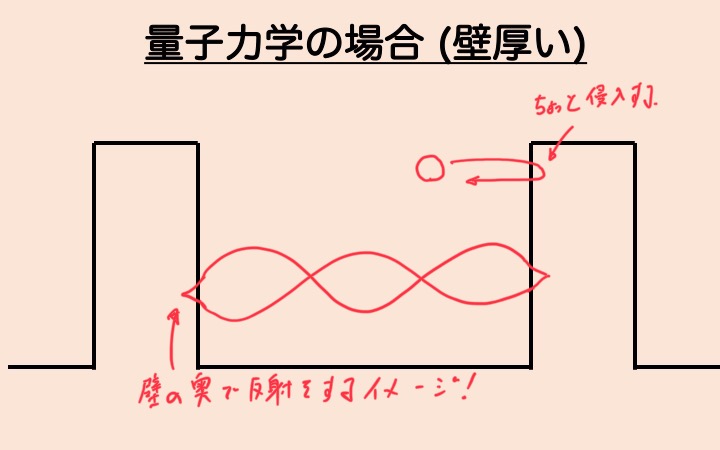
そこそこの厚みがあると、跳ね返りはするのですが、一部の粒子が壁に “染み出す” という現象が起きます。
この染み出しをイメージするには大変に難しいのですが、「数学的に、壁の中に存在していてもおかしくない」という結果が出た、みたいな感じです。
染み出したあとは、その粒子は壁の内部にとどまらずに跳ね返されます。
つまり、「壁の表面より、ちょっと内側で跳ね返る」粒子が、存在する(確率がある) ということです。
存在確率はこんな感じです!
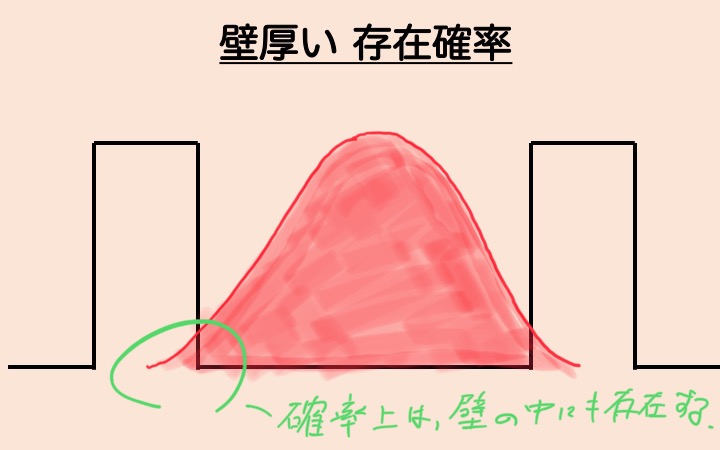
このイメージを持っておいてください。
しみ出して、「通り抜け」る
では、もっと薄い壁(ポテンシャル障壁) ではどうか?
※ちなみに薄い、というのが重要で、原子が数百個とか、分子が数十個とかだと思ってください。
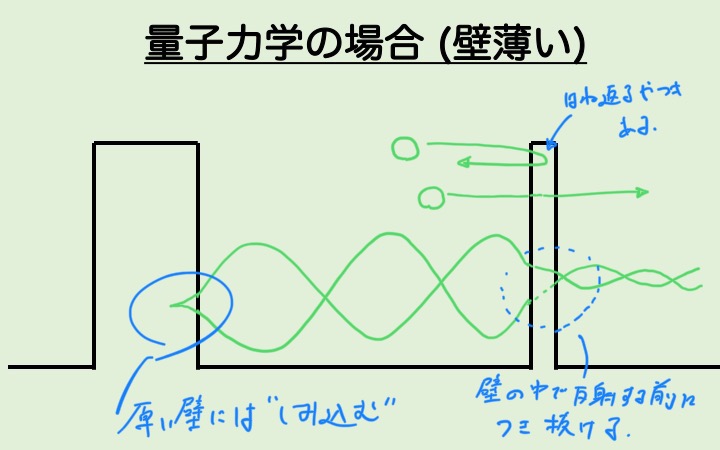
この時は、存在確率が0にならないうちに、その壁を突き抜けてしまいます。
こうなったらこっちのもので、もう跳ね返る必然性がないのでそのまま右に進んで行きます。
コレが、トンネル効果の正体です。
つまり、粒子が染み出して、ついには反対側に出たものが「通り抜けた」ということです!
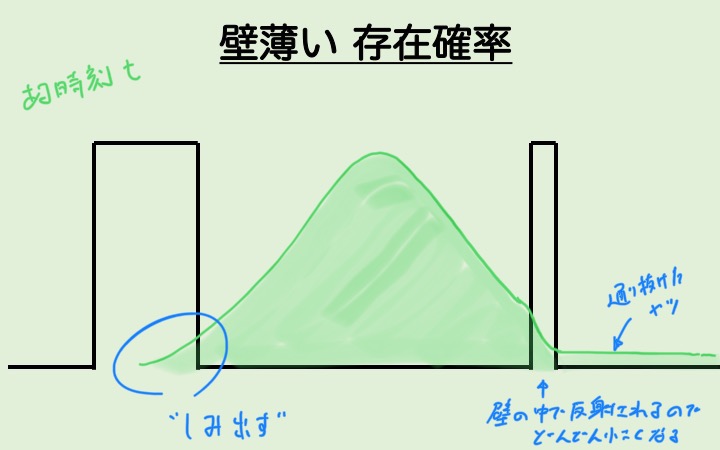
どのくらいすり抜けるかということですが、それは壁の厚さや粒子とポテンシャル障壁のエネルギー差などによってまちまちです。
ちなみに、「なんでこんなことが起きている」のかというのはなくて、「数学上ではこうなっていて、現実でもこうなっている」みたいな感じです。
事実、アインシュタインは量子力学の考え方を受け入れられず、「神はサイコロを振らない」などの名言を残したほど。
トンネル効果の身近な例
では、トンネル効果は生活のどのようなところに使われているのでしょうか?

と言いたいところだったのですが…
出てきたのが、以下のようなものでした。
- ダイオードにおける、トンネル接合
- 生物学における、プロトントンネリング
- 恒星内での核融合
コレが身近な人は… いないですよね?
まぁ、かなりミクロな話なので、私たちの生活で見ることができるのはあまりないということみたいです。
最後に:量子の世界は不思議がいっぱい
以上がトンネル効果の説明でした!
ちょっと複雑なのと、自分の説明の都合で省略・簡略化してしまったところが多いのですが、ざっくりとしたイメージは伝わったと思います。
こんな風に量子の世界は不思議なことがいっぱいあります。
しかも、最近はこうした技術を用いたデバイスが開発されたりしているので、技術職的にもワクワクします!
興味を持ってくれたなら、ぜひ「もう少しちゃんとした量子の本」を手にとってみることをお勧めします。
高校生くらいなら、ブルーバックスがちょうど良いですよ!
他にも、シュレーディンガーの猫なんかについて書いた記事もあるので、ぜひそちらも読んでみてください!
関連記事:京大生が “シュレーディンガーの猫” を世界一わかりやすく解説します