数学2において、最初の壁はラジアンだと思います。
急に新しく出てくるわりに何の説明もされずにすっ飛ばされてしまうことが多いので「文系に行けばよかった…」 と思う人が大量発生したりします。

この記事では、
- ラジアン(弧度法)って何?
- ラジアンと角度の変換
- ラジアンを使うメリット
- ラジアンを使った練習問題
と言うような内容について書いていきたいと思います。
タイトルの通り、数学が苦手な猫にもわかるように書いたのでぜひ読んでみてください!
目次 (クリックでジャンプ)
ラジアン(弧度法)って何?

まず、ラジアンとは何かと言うことについて簡単に説明しておきたいと思います。
ラジアンとは、ズバリ角度の単位のことです。
だから、1 ”度” と同じように 1 “ラジアン” と言う単位があるのです。
1の場合は、円を360分割して、それを360度として扱っています。では、ラジアンは何を持って1ラジアンというかというと…
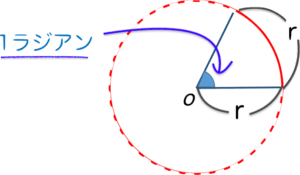
半径がr の円において、弧の長さがr の時の角度
のことを1ラジアン と呼びます。
図で書くとこんな感じですね。

と思う人もいるかもしれません…もうちょっと辛抱して読み進めてください。
ラジアンと角度の変換
ここで、よくわからんラジアンを度数に変換してみましょう。
1度と言うのは円を360°で分割しているので、1周で360°ですよね?では、ラジアンは何ラジアンで1周分でしょうか?
ラジアンは式で書くと $1ラジアン = \frac{円周}{半径} = \frac{1}{1} $ですね。では、1周分のことを考えてみると…
円周は2πrなので、1周分の角度は2π ラジアンになります。
つまり、360° = 2π ラジアンなのです。
度数とラジアンの対応は下図の通り。別にテストには出ませんが、感覚として “このくらい” と言うのは覚えておいたもいいかもしれません。
| 度数 (Degree) | ラジアン (rad) |
|---|---|
| 0° | 0 |
| 30° | π/6 |
| 45° | π/4 |
| 90° | π/2 |
| 180° | π |
| 360° | 2π |
※もちろん、代表値です。
ちなみに、ラジアンは単位と最初に言いましたが、省略されることが非常に多いです。 sin 2πのこの部分も単位はラジアンです。けど、省略されています。
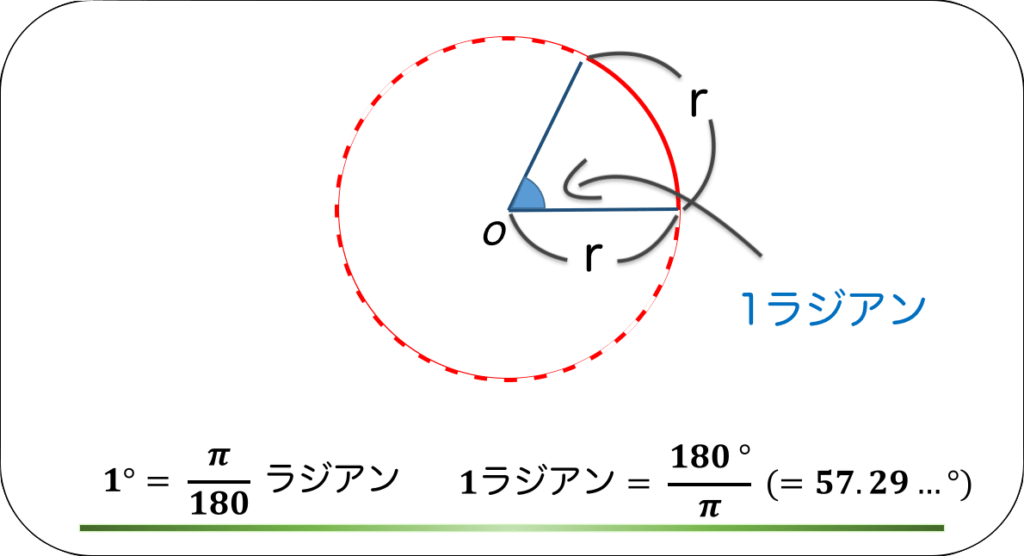
もう一度振り返ると、ラジアンというのは半径がr の円において、弧の長さがr の時の角度のことで、360°が2πラジアンに対応します。
ちなみに、覚えなくていいですが計算しておくと1ラジアンは約57°になります。
ラジアンを使うメリット
角度を度(degree) を使って表す方法を度数法、一方でラジアンを使って表す方法を弧度法と呼びます。
度数法を使うメリットは、単純にわかりやすいことです。360度なので時計の針とかで直感的にわかりやすいのと、子どもの頃から親しんでいるので体にインプットされていると言うのがあります。
では、なぜ弧度法なんていう一見めんどくさい方法をとるかというと
- 式がシンプルになる場合が多い
- 極限、微分をするときにやりやすい
というメリットがあるからです。
例えば、三角形の微分の公式に
$$ \frac{d}{dx} sin x = cos x $$
というものがあります。これは、弧度法で表しているのですが、これを度数法にするといちいちxを $\frac{180x °}{π}$ に変形しなくてはならなくなります。
では、なぜ度数法( °)がややこしくなって弧度法がシンプルになるかというと、それは弧度法がr(半径) に基づいて決められた距離 だからです。
詳しいことは数学の先生に聞いてもらえるといいのですが、基本的には円は半径だけが決められた図形です。なのでその半径を使うと無駄な数字が出てきにくいという性質があります。
度数法の方がいいという人もいるかもしれませんが、度数法って冷静に考えてみれば色々変なところが多いんです。そもそも、度数は何で360°なの? っていう話ですよね?
これは、度数法が生活の中で生まれた区切り方だということが大きいと思います。
でも、数学で使うにはあまりにややこしくて不便だったのです。そこで、このややこしい度数を使わないで済む方法を考えた結果、半径r を使ってラジアンで表現することによって見やすくしたのがラジアンというわけです。
ラジアンを使った練習問題

毎度のことなので、ラジアンについて軽く問題を出したいと思います。ラジアンのことがよくわかる問題です!
次の度数で表された角度を、ラジアンで示せ。ただし、単位をつけること
- 30°
- 135°
- 360°

度数からラジアンにするには $\frac{π}{180} $ をかければよかったので、答えは順番に
$\frac{π}{6} $ラジアン 、$\frac{3π}{4} $ラジアン 、$ 2π$ラジアンとなります。
sin 1 、sin 45° ではどちらが大きいか?
これ、定義を知らないと習いたての人はかなり難しい問題になると思います。
考え方だけいうと、角度を度数かラジアンかに合わせて考えて、π= 3.14… であることを使います。今回はせっかくなのでラジアンに合わせましょう。
sin 45° = sin π/ 4 であり、これは sin 0.785… です。そして、sin 90° = sin π/2 が一番大きいことを考えると、sin 1の方が大きいことがわかります。
ちなみに、1ラジアンが約54度ということがわかっていればすぐに解くことができる問題ですが、何回も行っているように覚えなくてもいいのでその場で解けるようにしましょう。
最後に:ラジアンは 360°= 2πだけ覚えよう
以上、数2で習う 弧度法(ラジアン) を猫でもわかるように解説してきました。これがわかったら、數2の壁を1つクリアしたと言ってもいいでしょう。
まとめると、最終的には次の定義さえ覚えておけば大抵の場合はどうにかなります。
360° [度] = 2π [ラジアン]
ラジアンは数学が進めば進むほど「理解して当たり前」という雰囲気が出てきます!
なのでまだモヤモヤしている人はぜひじっくり読み返して考え抜いてみてください!
また、青チャートやフォーカスゴールドなどの問題集で何度も解き直してみると理解度も上がっていくのでぜひ手を動かしてみてください!